May 2017 saw a spectacular lightning storm over the northern parts of the island. This amazing photo was captured by Adrian Cunningham. Lightning is probably the most impressive example of an electrostatic discharge that I know of. That it is caused by the movements of gazillions of tiny charged particles called electrons due to massive convection currents within a cloud really staggers me!
4.1 - Charges and Charging
Objectives:
- To know that electric charge is carried by the electron and proton and that they have a specific and discrete charge, e.
- To understand that macroscopic charge is due to electrons being moved from one place to another.
- To know how an object can be charged.
4.2 - Coulomb's Law (Recap - see 10.5)
Objectives:
- To know (learn!) the equation that describes the force that acts between two charges
- To be able to solve problems involving two or more charges interacting with each other.
Between any two charged particles there exists a force. If the charges are the same then this is a repulsive force, if they are different the force is attractive. The forces of each particle on the other are the same - Newton's 3rd Law - as it is a mutual force between the charges. The magnitude of the force, \(F\), between two electrically charged bodies, which are small compared with their separation, \(r\), is inversely proportional to the product of their charges, \(Q_{1}\) and \(Q_{2}\). and decreases as an inverse square law with distance.
\[F = \left ( \frac{1}{4\pi\epsilon_{0}} \right) \frac{Q_{1}Q_{2}}{r^{2}}\]
Unlike gravitational fields that can move through matter unaffected and cannot be shielded, electric forces are affected by the material through which they are propagating. The permittivity of a material can be conceptualised as a description of how hard or easy it is for an electrical field to move through the material.
The permittivity of free space is:
\[ \epsilon_{0}= 8.85 \times 10^{-12}\,\text{C}^{2} / \text{Nm}^{2}\]
The AP and US textbooks tend to replace the \(\frac{1}{4 \pi \epsilon_{o}}\) bit with a constant called \(k\). The justification is that it looks cleaner, is easier to enter into calculators and highlights the similarity with Newton's Law of Gravitation. While this has some merit, I feel that it tends to hide some useful conceptual ideas. The \(4 \pi\) bit is related to the surface area of a sphere (ask why?) and the \(\epsilon_{o}\) bit is a measure of how the electric field is transmitted through space. This permittivity and a similar concept for magnetic fields has a part to play later in the course.
\[k = 8.99\times 10^{9}\; \text{Nm}^2/\text{C}^{2}\]
US form of Coulomb's Law is:
\[F = k\frac{Q_{1}Q_{2}}{r^2}\]
\[F = \left ( \frac{1}{4\pi\epsilon_{0}} \right) \frac{Q_{1}Q_{2}}{r^{2}}\]
Unlike gravitational fields that can move through matter unaffected and cannot be shielded, electric forces are affected by the material through which they are propagating. The permittivity of a material can be conceptualised as a description of how hard or easy it is for an electrical field to move through the material.
The permittivity of free space is:
\[ \epsilon_{0}= 8.85 \times 10^{-12}\,\text{C}^{2} / \text{Nm}^{2}\]
The AP and US textbooks tend to replace the \(\frac{1}{4 \pi \epsilon_{o}}\) bit with a constant called \(k\). The justification is that it looks cleaner, is easier to enter into calculators and highlights the similarity with Newton's Law of Gravitation. While this has some merit, I feel that it tends to hide some useful conceptual ideas. The \(4 \pi\) bit is related to the surface area of a sphere (ask why?) and the \(\epsilon_{o}\) bit is a measure of how the electric field is transmitted through space. This permittivity and a similar concept for magnetic fields has a part to play later in the course.
\[k = 8.99\times 10^{9}\; \text{Nm}^2/\text{C}^{2}\]
US form of Coulomb's Law is:
\[F = k\frac{Q_{1}Q_{2}}{r^2}\]
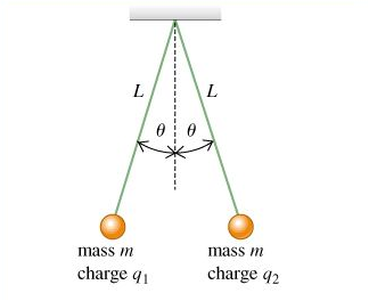
Experimental Work
Coulomb's Law leads to some pretty weak forces between the charges that we are able to produce in the lab. The classic experiment is to suspend two very light pith balls that have been painted with conducting material from lengths of cotton. Once they are charged up they repel and the force between them can be deduced from the angle that they stabilize at. This requires the use of statics from Unit 2. It is next to impossible to measure the charges on the spheres, so instead we calculate the product of the charges and see if they are realistic. Usually microcoulombs. To do a proper investigation that can yield a graph and a value for the electrostatic constant, k, or the permittivity of air, epilson_naught, we have to resort to a computer simulation. An excellent one has been created by the ever-resourceful Physics Aviary website.
Coulomb's Law leads to some pretty weak forces between the charges that we are able to produce in the lab. The classic experiment is to suspend two very light pith balls that have been painted with conducting material from lengths of cotton. Once they are charged up they repel and the force between them can be deduced from the angle that they stabilize at. This requires the use of statics from Unit 2. It is next to impossible to measure the charges on the spheres, so instead we calculate the product of the charges and see if they are realistic. Usually microcoulombs. To do a proper investigation that can yield a graph and a value for the electrostatic constant, k, or the permittivity of air, epilson_naught, we have to resort to a computer simulation. An excellent one has been created by the ever-resourceful Physics Aviary website.
|
\[F\uparrow=F\downarrow\]
\[L\cos\theta=mg\] \[F\leftarrow=F\rightarrow\] \[F_{e}= L\sin\theta\] solving the simultaneous equations yields: \[F_{e}= mg\tan\theta\] |
4.3 - Electric Field Strength
Objectives:
- To be able to describe the concept of electric fields.
- To be able to calculate the electric field strength surrounding a point charge.
- To be able to calculate the electric field strength between two charged plates.
- To be able to calculate the force on a point charge due to an electric field.
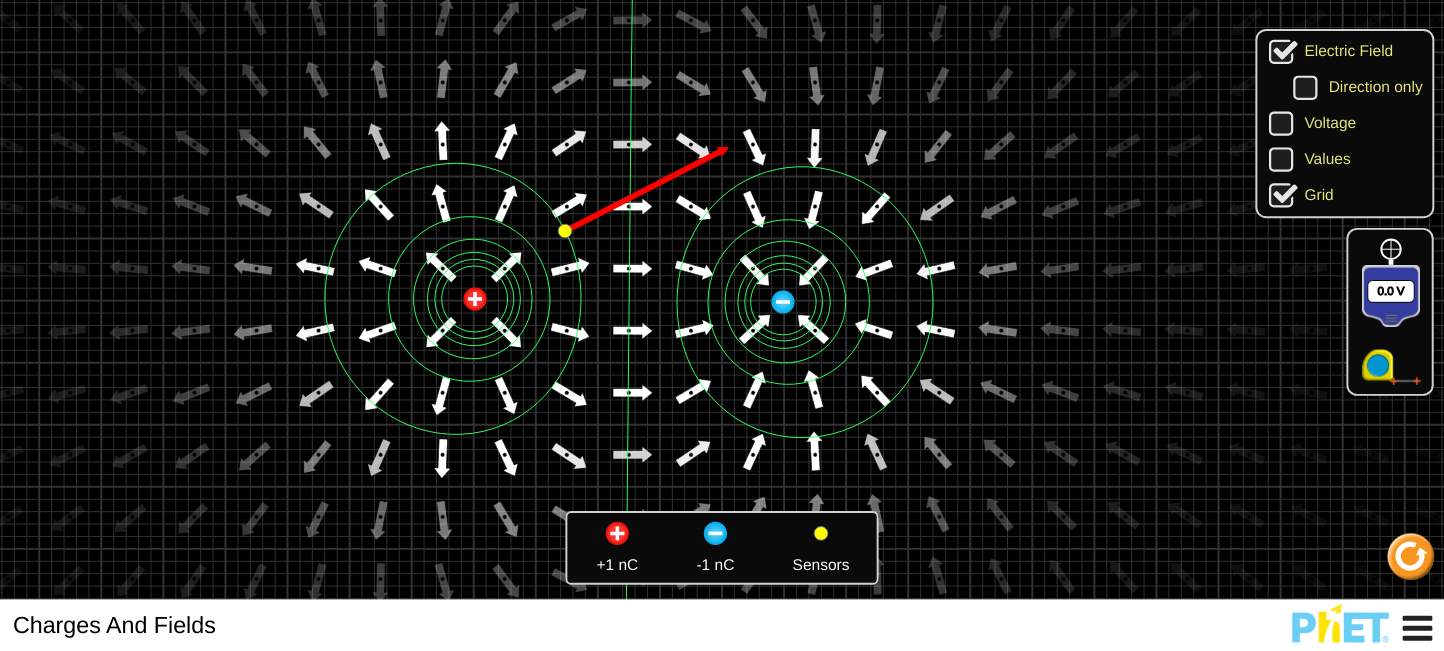
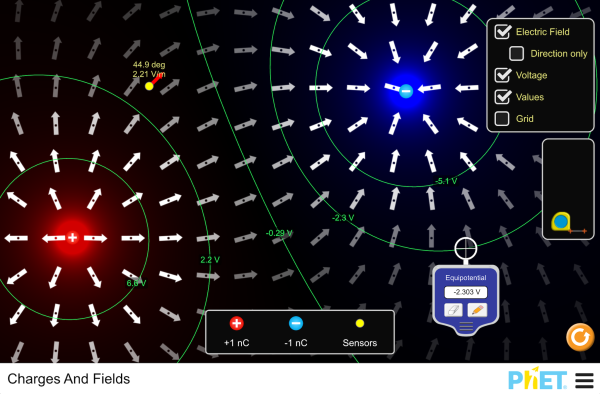
The force between two charges is derived from Coulomb's Law above. A force field is a region of space surrounding something that causes a force. There are three force fields that we deal with in AP Physics: Gravity, Electric and Magnetic fields. We define the electric force field as the force due to the field on a +1.0 C of charge. The PhET simulations below are excellent ways to visualise these fields and you are strongly encouraged to use them. Mathematically, we define the field strength as the force per unit charge. There are two configurations that we commonly come across, the field around point charges and the field due to parallel plates.
Point Charges.
Point Charges.
\[E=\frac{kQ}{r^{2}}\]
\[E=\frac{V}{d}\]
4.4 - Millikan's Oil Drop Experiment
Objectives:
- Know how to calculate the electric field strength between two charged plates.
- Know the basics of the Millikan Oil Drop Experiment
The Millikan Oil Drop experiment is one of the classic experiments to learn. From careful analysis of his results, Robert Millikan determined that charge is quantised - can only have a set number of values. This is fundamentally due to the fact that all protons and electrons have the same magnitude of charge, e. An object is charged because a deficit or surplus of these particles, so can only have integer values of e as their charge. It was a key constant to pin down as so much else depends on it.
Millikan Oil Drop Simulation - Teach Science, this is a classic simulation that I have used for years. Only runs on Windows. It has two modes - the easiest is to use the 'beads', which sets the oil droplets to a fixed mass. This greatly simplifies the experiment as then the analysis reduces to balancing the weight of the droplet by adjusting the voltage of the plates. In reality, Millikan could not easily determine the mass of the droplet. He measured its terminal velocity and used this to get a value for the mass of the droplet (see worksheet). Then, before the droplet hit the bottom, he switched on the voltage and suspended the droplet to measure its charge. The amazing thing was that he found that the droplets all had charges that were multiples of the fundamental electron charge, \(e\).
\[e = 1.6\times 10^{-19}\, \text{C}\]
\[e = 1.6\times 10^{-19}\, \text{C}\]
LAB 13.2 - Millikan Simulation (easy)
LAB 13.2A - Millikan Simulation (advanced)
HW 13.3 - Millikan's Oil Drop
LAB 13.2A - Millikan Simulation (advanced)
HW 13.3 - Millikan's Oil Drop
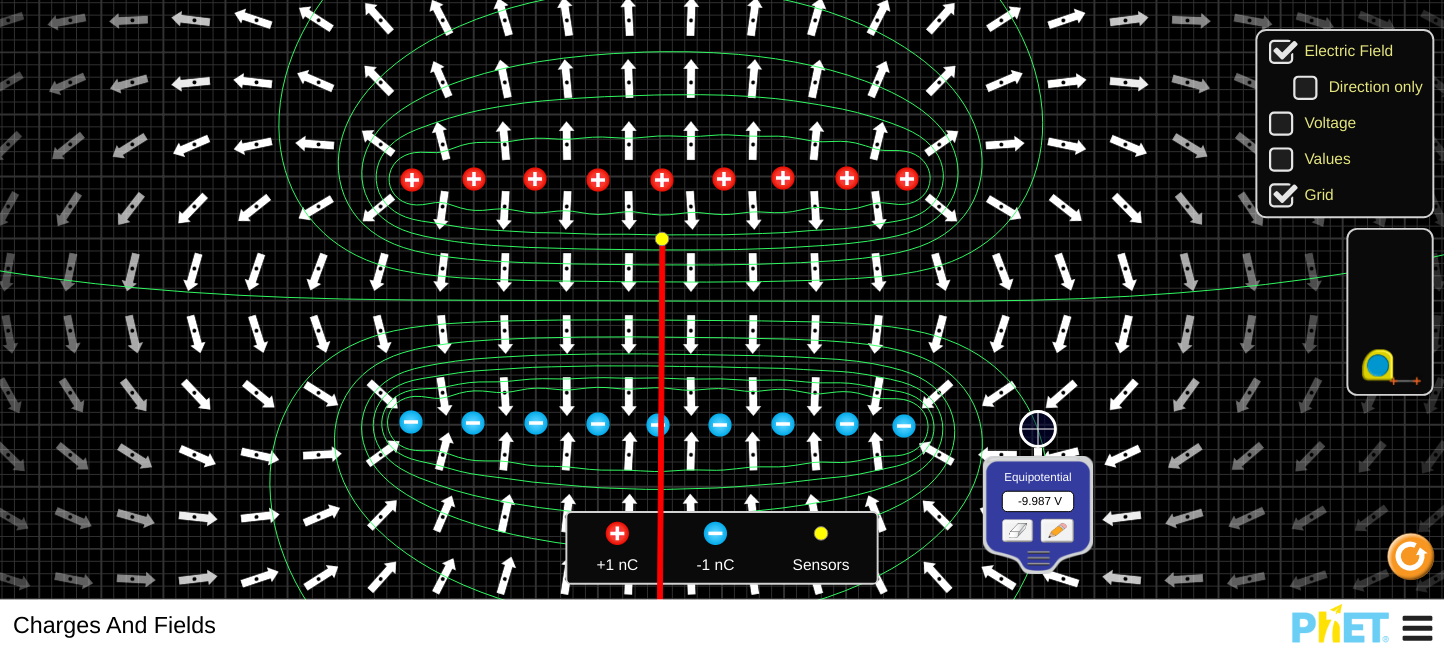
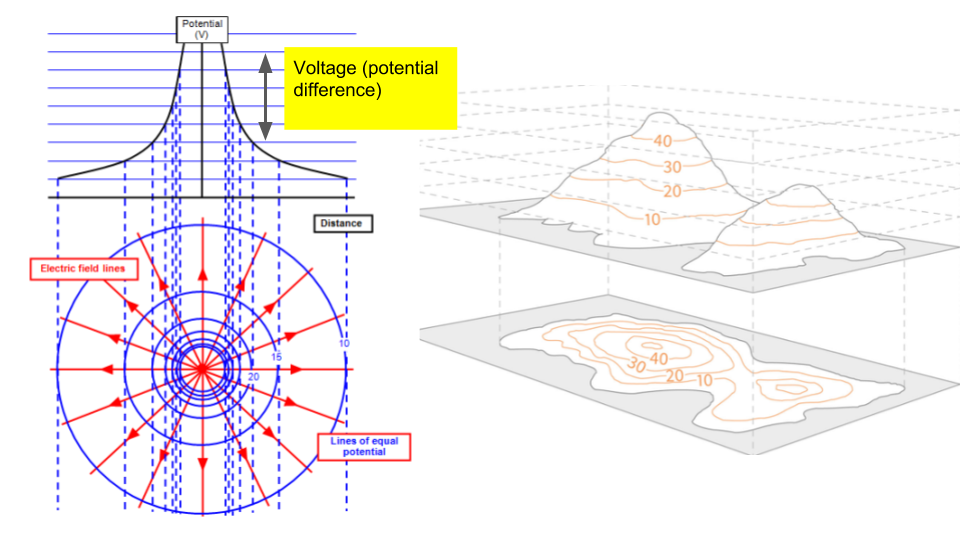
4.5 - Electric Potential
Objectives:
- Understand the concept of electric potential and be able to draw equipotentials.
- To be able to calculate the electric potential due to a point charge.
- To be able to calculate the electric potential between two point charges.
- To be able to describe an electron gun and to be able to calculate the speed of an accelerating electron.
Physics Aviary - Electrical Potential Energy Problems. (you will need scratch paper before attempting these)
Physics Aviary - Virtual Lab : closest point of approach. Requires understanding of energy.
Electrostatic Energy - two major concepts.
Electrical Energy = work done to move a charged particle in an E-field from infinity to its current location.
**** Be careful not to get the symbols for energy and electric field strength mixed up ****
Point charges
Based on the basic concept that the potential energy is the energy stored from the work done, which is the application of a force over a distance and then substituting the equations for force, we get:
\[W = F\Delta x\]
\[PE = qEr\]
\[PE = k\frac{Qr}{r}\]
Electrical Energy = work done to move a charged particle in an E-field from infinity to its current location.
**** Be careful not to get the symbols for energy and electric field strength mixed up ****
Point charges
Based on the basic concept that the potential energy is the energy stored from the work done, which is the application of a force over a distance and then substituting the equations for force, we get:
\[W = F\Delta x\]
\[PE = qEr\]
\[PE = k\frac{Qr}{r}\]
The big take-away here is that the potential energy drops away inversely proportional to the distance rather than an inverse-square relationship.
Parallel Plates
Again - starting from the basic definition of work, but this time using the electric field of a parallel plate equation \(E=\frac{V}{d}\) we get:
\[PE = qEd = qV\]
Again - starting from the basic definition of work, but this time using the electric field of a parallel plate equation \(E=\frac{V}{d}\) we get:
\[PE = qEd = qV\]
Recall the work-energy theorem - that work is converted to KE, so if a charged particle is accelerated from rest by a voltage, its electrical potential energy will be converted to kinetic energy. This will give us the speed of the particle. This is commonly used in particle accelerators such as the straightforward electron gun.
So why is this useful? If we know either the electric field strength or the potential difference across a field, we can calculate the speed of an accelerated particle due to that field. ** This is absolutely essential for ANY studies on atomic and nuclear physics! **
If we have the moving charge set to \(+1\,\text{C}\), then we starting talking about "potential" rather than specifically potential energy. The difference between the potentials at two locations is known as the potential difference (aka voltage). It is the difference in potential energy of a \(1\,\text{C}\) charge, so units are \(\text{J/C}\) (aka Volts). This is the origin of why physics teachers call the voltage of a battery 'potential difference'. The energy supplied by a battery to each coulomb of electrons is the voltage.
\[\Delta KE = W = eV\]
So why is this useful? If we know either the electric field strength or the potential difference across a field, we can calculate the speed of an accelerated particle due to that field. ** This is absolutely essential for ANY studies on atomic and nuclear physics! **
If we have the moving charge set to \(+1\,\text{C}\), then we starting talking about "potential" rather than specifically potential energy. The difference between the potentials at two locations is known as the potential difference (aka voltage). It is the difference in potential energy of a \(1\,\text{C}\) charge, so units are \(\text{J/C}\) (aka Volts). This is the origin of why physics teachers call the voltage of a battery 'potential difference'. The energy supplied by a battery to each coulomb of electrons is the voltage.
\[\Delta KE = W = eV\]
example: an electron is accelerated by \(5000\, \text{V}\). We can use the above to determine its speed as it hits the positive plate:
\[\frac{1}{2}mv^{2}=eV\]
\[v^{2}=\frac{2eV}{m}\]
\[v=\sqrt{\frac{2\times 1.6\times 10^{-19}\times 5000}{9.11\times10^{-31}}}\]
\[v= 4.19\times 10^{7} \; \text{m}/\text{s}\]
\[\frac{1}{2}mv^{2}=eV\]
\[v^{2}=\frac{2eV}{m}\]
\[v=\sqrt{\frac{2\times 1.6\times 10^{-19}\times 5000}{9.11\times10^{-31}}}\]
\[v= 4.19\times 10^{7} \; \text{m}/\text{s}\]
It is very common to get into a mess with the SIGNS
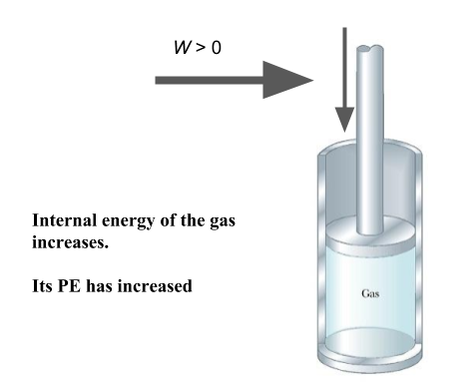
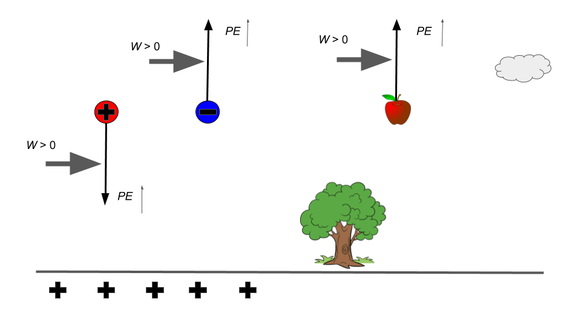
If the PE decreases due to the ‘natural’ motion of the object (e.g. repelled) then the change in PE is negative, it loses PE. Because it has done Work on the surroundings, If the charged is forced against its ‘will’. E.g. a positive charge pushed towards another positive charge, work has gone INTO the system and its PE will increase. (remember thermo)
(caveat - this is only true for CONSERVATIVE forces where the PE can be recovered as KE when the system is released. The most famous example of a non-conservative force is friction. Any work done against friction is lost as heat and not stored as PE, so no KE is recoverable. Strictly speaking, the gas piston compression is only conservative if no heat is lost (adiabatic), but the linking concept is still useful.
If the PE decreases due to the ‘natural’ motion of the object (e.g. repelled) then the change in PE is negative, it loses PE. Because it has done Work on the surroundings, If the charged is forced against its ‘will’. E.g. a positive charge pushed towards another positive charge, work has gone INTO the system and its PE will increase. (remember thermo)
(caveat - this is only true for CONSERVATIVE forces where the PE can be recovered as KE when the system is released. The most famous example of a non-conservative force is friction. Any work done against friction is lost as heat and not stored as PE, so no KE is recoverable. Strictly speaking, the gas piston compression is only conservative if no heat is lost (adiabatic), but the linking concept is still useful.
4.6 - Capacitors
Objectives:
- Know how two parallel plates can store charge as a capacitor.
- To know and be able to use to the equation for the capacitance of a capacitor.
- To be able to calculate the energy stored by a capacitor
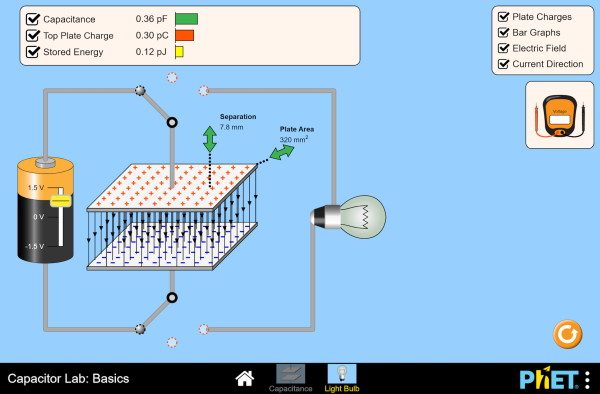
Capacitors are electrical devices that can store charge on two metal plates that are separated by an insulator. In some respects they behave a bit like a rechargeable battery in that they can be charged up, store that charge until such time as they are discharged. But the similarity ends there. Batteries are chemical devices and can store a lot of charge that can be steadily discharged over a long time, whereas capacitors are purely physical devices that charge and discharge exponentially. Simply put, when two large plates are connected to a battery, the battery pulls electrons from one plate and puts them on the other plate until the potential difference (voltage) across the plates equals that of the battery. Thus, there is a small burst of current even though there is not a complete circuit.
The amount of charge, Q, that can be shifted from one plate to the other per volt is known as the capacitance, C. The unit is the Farad (F), which is a huge unit. Normal capacitors are in the picofarad to microfarad range.
\[Q=CV\]
The amount of charge, Q, that can be shifted from one plate to the other per volt is known as the capacitance, C. The unit is the Farad (F), which is a huge unit. Normal capacitors are in the picofarad to microfarad range.
\[Q=CV\]
This ability to store charge, its capacitance, depends on three variables: area of the plates, the separation of the plate and the nature of the insulator between the plates. At AP this is usually set to being air.
\[C = \epsilon _{o}\frac{A}{d}\]
\[C = \epsilon _{o}\frac{A}{d}\]
The dependance on the area seems obvious, if you have larger plates then more electrons can be shifted from/onto them. The dependance on the distance between the plates is less clear. Ultimately it is down to the strength of the electric field (E = V/d) between the plates. The stronger the electric field, the higher the ability to store charge. Using the PhET simulation below and playing attention to the electric field lines while changing other variables helps to reinforce this. As for the epsilon quantity, this is a constant of nature that relates how well an electric field can pass through a vacuum (free space). If another material is added between the gap, there is a multiplier that needs to be included. For example wax has a relative permittivity of 20 and makes for a much better capacitor than using air. The permittivity of air is almost exactly the same as for a vacuum.
Like a battery, if charge is separated and stored, we have also stored energy. This was the work done to move the electrons from one plate to another by the battery. It is the area under the charge/voltage graph and is easily remembered as it fits the usual pattern for energy equations!
\[E_{cap}=\frac{1}{2}CV^{2}\]
Like a battery, if charge is separated and stored, we have also stored energy. This was the work done to move the electrons from one plate to another by the battery. It is the area under the charge/voltage graph and is easily remembered as it fits the usual pattern for energy equations!
\[E_{cap}=\frac{1}{2}CV^{2}\]
|
This is a great simulation. It really helps to visualize the charges and the electric field between the plates, and how changing the voltage, separation and area make a huge difference. The one thing that it doesn't do is to allow you to change the dielectric material between the plates - but that is small potatoes.
If you are observant, it is possible to see the short bursts of a current when the plates are initially charged, and when the capacitor is altered in any way. |
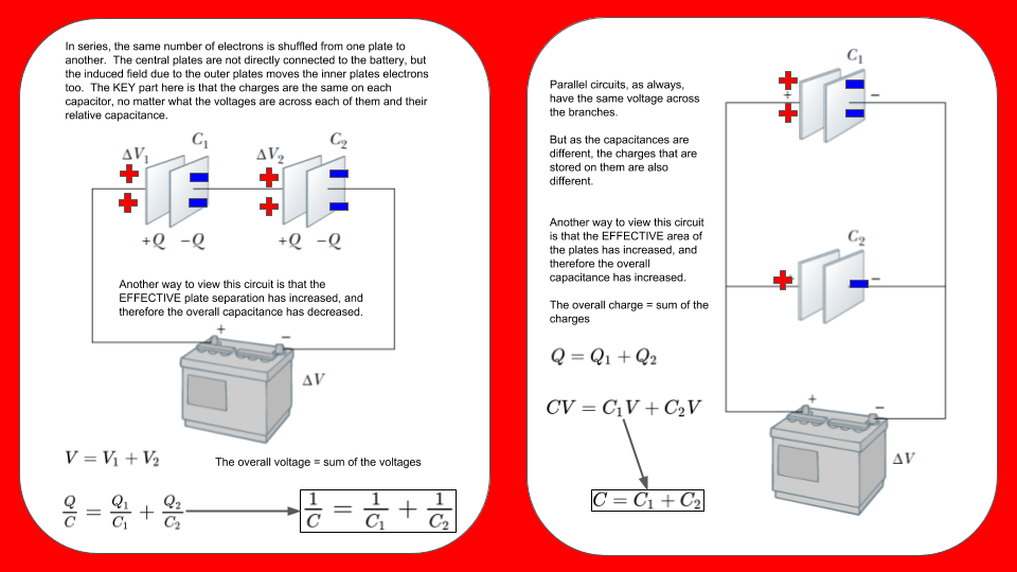
Capacitor Combinations
Just as with resistors we frequently have more than one capacitor and the basic configuration is either series or parallel. The equations are easy to learn, they are the same as springs and the opposite to resistors. That is not the problem - the problem is learning the justification, as this is often useful for multiple choice questions.
Just as with resistors we frequently have more than one capacitor and the basic configuration is either series or parallel. The equations are easy to learn, they are the same as springs and the opposite to resistors. That is not the problem - the problem is learning the justification, as this is often useful for multiple choice questions.
HW 13.6 - MC Questions