The International Space Station (Image: NASA)
3.1 - Circular Motion
Objectives:
- Be able to relate period, frequency and velocity for an object moving in a circle.
- Understand that a force directed towards the centre is required to force an object to move in a circular path.
- To be able to use the centripetal force equation.
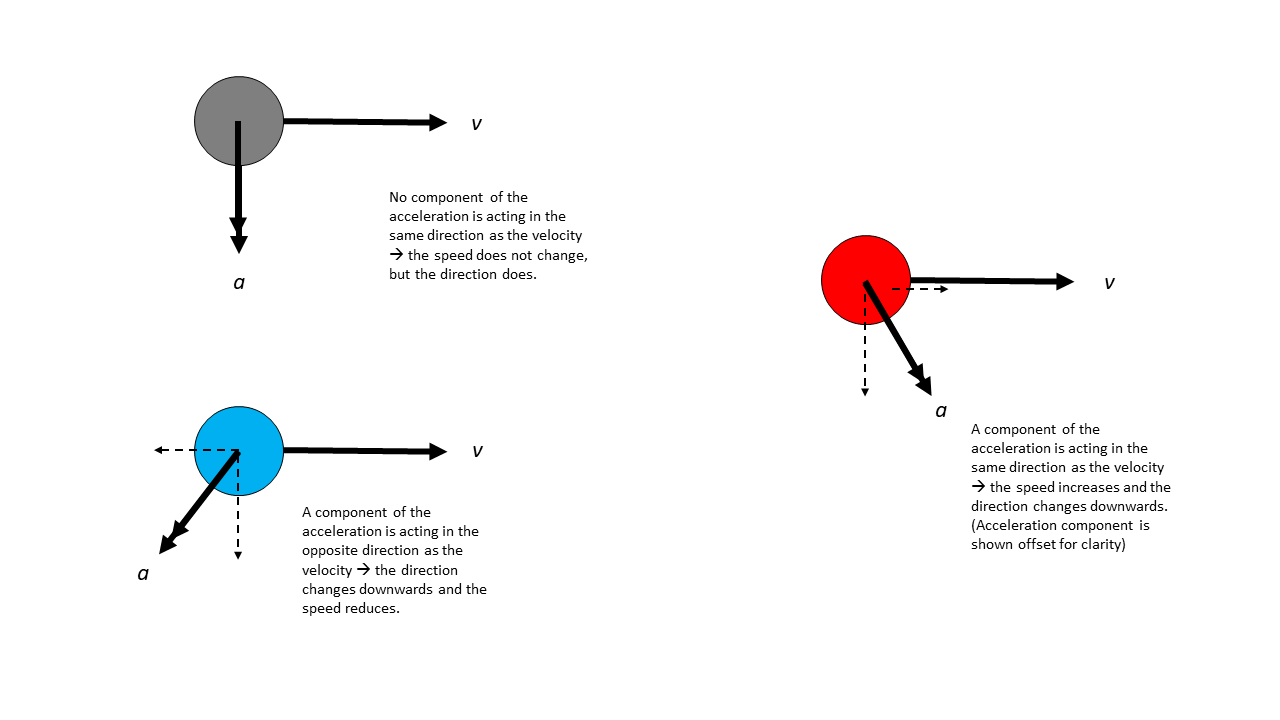
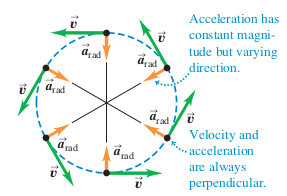
An object moved in a circular path if it is subject to a force that is perpendicular to its velocity. The force causes the object to accelerate without increasing its speed. As long as the force stays perpendicular to the velocity vector, the path with continue to be a circle. Note: the radius of a circle is ALWAYS perpendicular to a tangent at the point where the radius meets the circumference. If the acceleration vector was not perpendicular to the velocity vector, then the speed would change as well as the object's direction. The motion would not be circular.
Diagram to show why the acceleration MUST be perpendicular to the velocity to get circular motion. The scenarios for the red and blue balls will result in an elliptical path.
|
|
Centripetal Force
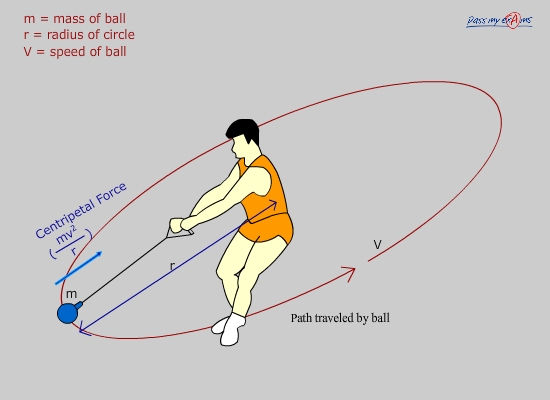
From Newton's Second Law, the inwards acceleration must be caused by a resultant force. The force that is required to pull an object around in a circle is known as the centripetal (centre-seeking) force. It's value can be calculated by the equation below. NOTE: this is not a new 'magic' force, it is the description of the size of ANY force necessary for circular motion. The force is provided by a standard force such as: tension (as in the rope in the diagram), gravity, electrostatic force, lift, the normal force, friction or a magnetic field. If the size and direction of this force is equal to that required for circular motion, the affected object will move in a circle. \[F = \frac{mv^{2}}{r}\]
The speed of an object moving in a circle can be easily determined by measuring the radius of the circle and the time it takes to complete a complete revolution. This time is known as the PERIOD.
\[v=\frac{2 \pi r}{T}\]
Common error: students often think that the centripetal force is a special force. It is not. It is just whatever force happens to be providing the inwards pull to cause the circular motion.
From Newton's Second Law, the inwards acceleration must be caused by a resultant force. The force that is required to pull an object around in a circle is known as the centripetal (centre-seeking) force. It's value can be calculated by the equation below. NOTE: this is not a new 'magic' force, it is the description of the size of ANY force necessary for circular motion. The force is provided by a standard force such as: tension (as in the rope in the diagram), gravity, electrostatic force, lift, the normal force, friction or a magnetic field. If the size and direction of this force is equal to that required for circular motion, the affected object will move in a circle. \[F = \frac{mv^{2}}{r}\]
The speed of an object moving in a circle can be easily determined by measuring the radius of the circle and the time it takes to complete a complete revolution. This time is known as the PERIOD.
\[v=\frac{2 \pi r}{T}\]
Common error: students often think that the centripetal force is a special force. It is not. It is just whatever force happens to be providing the inwards pull to cause the circular motion.
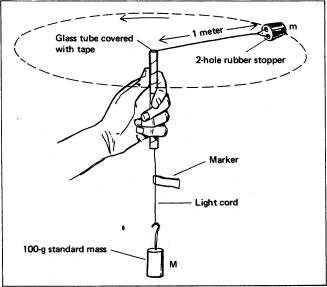
LAB WORK: We will be demonstrating the centripetal force equation empirically, i.e. by experiment. The centripetal force will be provided by the suspended masses, \(Mg\). You will be timing how long it takes the bung to complete \(10\) revolutions and using this to determine the speed. By plotting \(v^2\) against either the radius, \(r\), or the force variable, \(F\), we should find that the data is linear.
QUESTION: Why time for \(10\) revolutions instead of just a single one?
QUESTION: Why time for \(10\) revolutions instead of just a single one?
Worked Examples
The roundabout at the Foot of the Lane, Bermuda. Based on Google Earth the radii of the centre of the lanes are 12.8m and 16.2 m. Image: Bernews
|
Free-body diagram of a car cornering. Note that this has been simplified. There are actually 4 normal forces and 4 frictional forces - for each wheel. This does not affect the final result.
|
Roundabouts
The photo above shows a major roundabout just outside of Hamilton. It is known by a few names; Foot of the Lane, Crow Lane and, more recently, Johnny Barnes roundabout after the late old guy that used to stand and wave to commuters every morning. This is the scene for many traffic accidents, usually for the following reasons: texting, speeding and drinking. Often in combination. Here I am going to calculate the maximum theoretical speed that a vehicle can successfully execute the roundabout in both dry and wet conditions. (Of course, this is theory - don't go and try this out and crash....!)
Data: radius \(r=12.8\,\text{m}\), coefficient of static friction between rubber and dry tarmac, \(\mu = 0.7\). The mass of the vehicle is not important (surprisingly!)
The photo above shows a major roundabout just outside of Hamilton. It is known by a few names; Foot of the Lane, Crow Lane and, more recently, Johnny Barnes roundabout after the late old guy that used to stand and wave to commuters every morning. This is the scene for many traffic accidents, usually for the following reasons: texting, speeding and drinking. Often in combination. Here I am going to calculate the maximum theoretical speed that a vehicle can successfully execute the roundabout in both dry and wet conditions. (Of course, this is theory - don't go and try this out and crash....!)
Data: radius \(r=12.8\,\text{m}\), coefficient of static friction between rubber and dry tarmac, \(\mu = 0.7\). The mass of the vehicle is not important (surprisingly!)
|
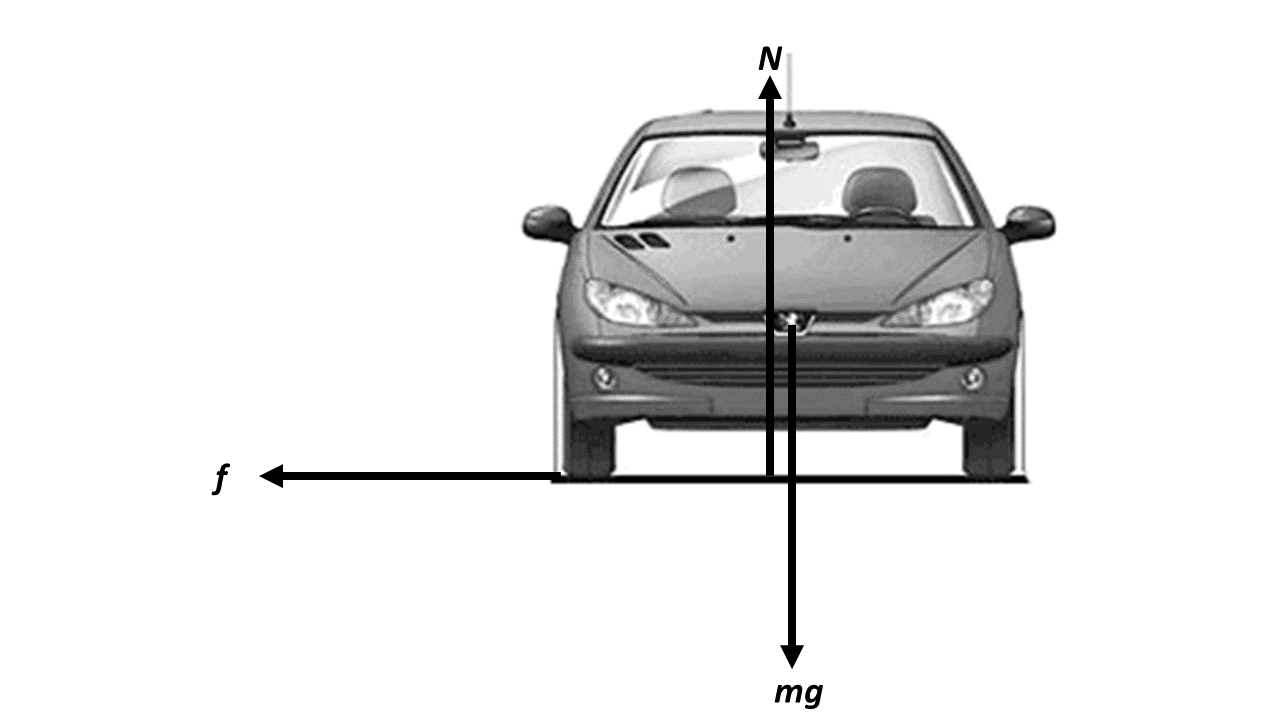
There is no change in motion in the vertical direction, so this is a statics situation.
\[F\uparrow = F\downarrow\] \[N = mg\] |
There is an inwards acceleration, so this is a dynamics situation.
\[\sum{F} = ma\] \[f=\frac{mv^2}{r}\] \[\mu N = \frac{mv^2}{r}\] |
Combining these two simultaneous equations gives us:
\[\mu mg = \frac{mv^2}{r}\]
Mass cancels and a bit bit of algebra gives us the maximum velocity when \(f=\mu N\):
\[v=\sqrt{\mu rg}\]
\[v =\sqrt{0.7\times 12.8\times 9.81} = 9.4 \,\text{m/s}=33.8\,\text{km/h}\]
For wet roads, this reduces to \(25.5\,\text{km/h}\).
\[\mu mg = \frac{mv^2}{r}\]
Mass cancels and a bit bit of algebra gives us the maximum velocity when \(f=\mu N\):
\[v=\sqrt{\mu rg}\]
\[v =\sqrt{0.7\times 12.8\times 9.81} = 9.4 \,\text{m/s}=33.8\,\text{km/h}\]
For wet roads, this reduces to \(25.5\,\text{km/h}\).
AP-1 type of questions. The sort of thing that they could ask you to explain are:
a) the car is moving, so why are we considering the coefficient of STATIC friction and not that of kinetic friction?
b) explain what would be the effect on the maximum speed for the curve if the radius were i) halved and ii) doubled?
a) the car is moving, so why are we considering the coefficient of STATIC friction and not that of kinetic friction?
b) explain what would be the effect on the maximum speed for the curve if the radius were i) halved and ii) doubled?
|
The "Wall of Death" - how does this work?
a) what upwards force prevents the bike falling down? b) what provides this force? c) what force pushes him into circular motion? |
|
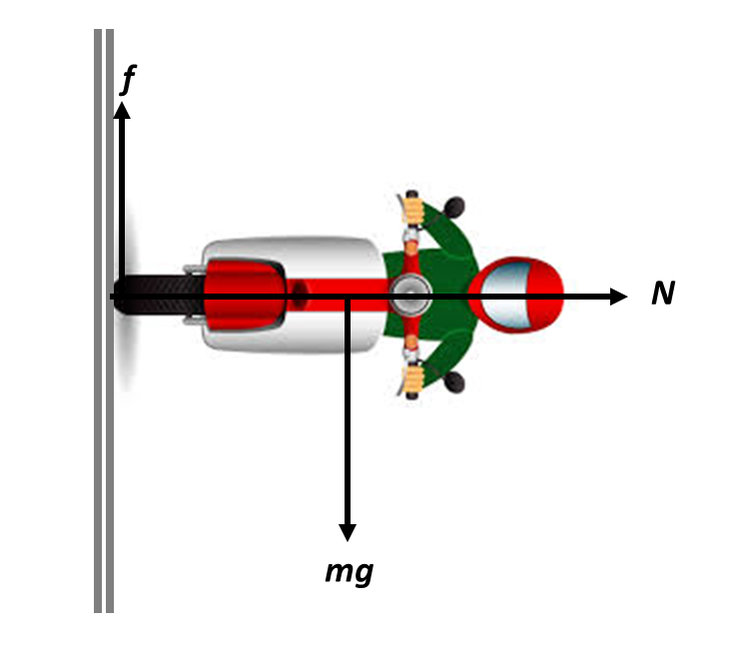
Based on the video, I estimate that the radius of the wall of death is \(6\,\text{m}\). The mass of the bike is unknown, so probably not too important? The walls are wooden and a quick google search tells me that the coefficient of friction between rubber and wood is not simple as there are many variables, but let's use \(0.5\) as a rough value. A quick free-body diagram reveals that the centripetal acceleration is provided by the normal force and that friction is counterbalancing weight. Top tip for figuring out the direction of friction - what would happen if there was no friction? In this case the bike would slide down the wall.
(As we will find out from Unit 7 - Rotational Mechanics, the force-pair of weight and friction exert a torque on the rider, so she probably has to lean the bike slightly upwards to compensate for this.)
(As we will find out from Unit 7 - Rotational Mechanics, the force-pair of weight and friction exert a torque on the rider, so she probably has to lean the bike slightly upwards to compensate for this.)
|
The vertical motion is constant - so static situation
\[F\uparrow = F\downarrow\] \[f=mg\] \[\mu N = mg\] |
The horizontal motion is changing, so dynamic situation.
\[\sum{F} = ma\] \[N = \frac{mv^2}{r}\] |
Combining these simultaneous equations gives:
\[\mu \frac{mv^2}{r} = mg\]
Mass cancels and we get:
\[v=\sqrt{\frac{rg}{\mu}}\]
Substituting my estimated values leads to:
\[v=\sqrt{\frac{9.81 \times 6}{0.5}}=10.8\,\text{m/s}=39\,\text{km/h}\]
\[\mu \frac{mv^2}{r} = mg\]
Mass cancels and we get:
\[v=\sqrt{\frac{rg}{\mu}}\]
Substituting my estimated values leads to:
\[v=\sqrt{\frac{9.81 \times 6}{0.5}}=10.8\,\text{m/s}=39\,\text{km/h}\]
|
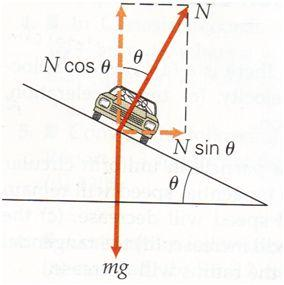
How does banking a curve help with cornering?
The idea behind banking a curve is to reduce the sideways friction required to make the turn drop to zero. Then there is no need to turn the front wheel(s) of the car or bike, and the vehicle will make the turn no matter how wet the road is, as long as it does not exceed the maximum speed that the curve was designed at. As weight is always acting vertically downwards, it cannot contribute to the centripetal acceleration. But the normal can. The limiting situation occurs when the horizontal component of the normal force can provide the entire centripetal force required. |
|
|
There is no change in motion in/out of the road, so this is a static situation:
\[F\uparrow=F\downarrow\] \[N\cos{\theta} = mg\] \[N=\frac{mg}{cos{\theta}}\] |
\[\sum{F}=ma\]
\[N\sin{\theta}=\frac{mv^2}{r}\] |
Combining the simultaneous equations gives us:
\[\frac{mg\sin{\theta}}{\cos{\theta}} = \frac{mv^2}{r}\]
Mass cancels, and assuming a maximum designed speed of (say) \(50\,\text{km/h} = 13.9\,\text{m/s}\) and a radius of \(15\,\text{m}\), we get a banking angle of:
Recall that \(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
\[\tan{\theta} = \frac{v^2}{rg}\]
\[\tan{\theta}=\frac{(13.9 \times 13.9)}{(15\times 9.81)}\]
\[\theta = 52.7^{\circ}\]
It is not only road vehicles that benefit from banked turned, but aircraft do as well. It is much more efficient to turn a plane by banking and using the a horizontal component of the lift from the wings to provide the force for the turn rather than use the tail mounted rudder. One thing that the pilots need to be aware of is that the vertical component of lift that holds the plane up in the air is reduced, so the plane descends slightly. The steeper the banking angle, the greater the loss of vertical lift but the tighter the radius of turn can be. A US Airforce B52 crashed a few years at an airshow by forgetting this.
\[\frac{mg\sin{\theta}}{\cos{\theta}} = \frac{mv^2}{r}\]
Mass cancels, and assuming a maximum designed speed of (say) \(50\,\text{km/h} = 13.9\,\text{m/s}\) and a radius of \(15\,\text{m}\), we get a banking angle of:
Recall that \(\tan{\theta}=\frac{\sin{\theta}}{\cos{\theta}}\)
\[\tan{\theta} = \frac{v^2}{rg}\]
\[\tan{\theta}=\frac{(13.9 \times 13.9)}{(15\times 9.81)}\]
\[\theta = 52.7^{\circ}\]
It is not only road vehicles that benefit from banked turned, but aircraft do as well. It is much more efficient to turn a plane by banking and using the a horizontal component of the lift from the wings to provide the force for the turn rather than use the tail mounted rudder. One thing that the pilots need to be aware of is that the vertical component of lift that holds the plane up in the air is reduced, so the plane descends slightly. The steeper the banking angle, the greater the loss of vertical lift but the tighter the radius of turn can be. A US Airforce B52 crashed a few years at an airshow by forgetting this.
|
|
Circular Runways - great idea! (although not in Bermuda....)
What causes the circular motion in this case? |
|
|
|
Other Resources
PhET Simulation - Balancing Act
PhET Simulation - Gravity and Orbits
|
|
|