|
Energy >>
|
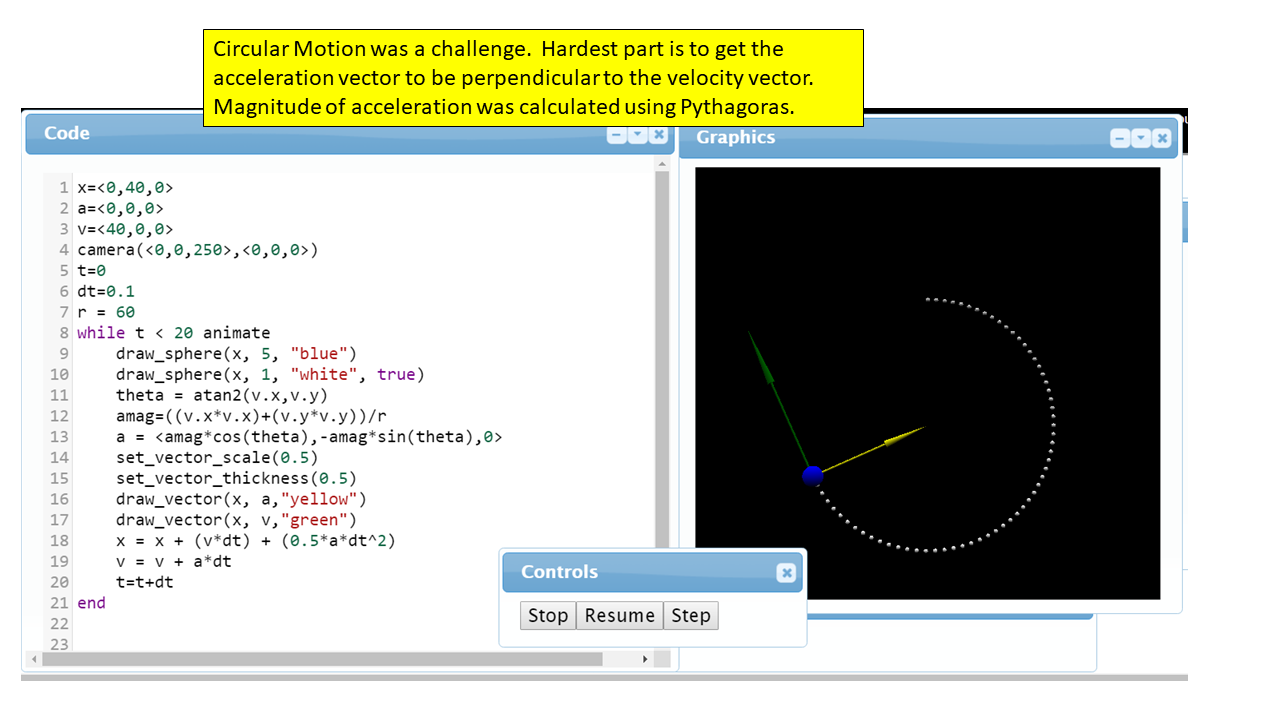
This is a difficult one. The key to circular motion is that the force acts perpendicular to the velocity. There is not an easy way to do this. My solution was to get a pencil and paper and sketch out the vectors and their components. The magnitude of the force vector is easy - simply use Pythagoras to get the magnitude of the velocity and use: \[F = \frac{mv^2}{r}\]
Then this needs to be multiplied by a unit vector that is perpendicular to the velocity. There may be easier or better ways to do this, but my solution involved geometry. I calculated the angle of the velocity vector using \(\tan\theta = \left(\frac{v_x}{v_y}\right)\) and I set the unit acceleration vector to \(a=\,<\cos\theta,\sin\theta,0>\).
My issue is that there has to be a better method of producing a centre-seeking force. I would prefer to define a central point and have a force vector directed at that point. After all, planets do not orbit because their acceleration is perpendicular to their velocity, but because the force that causes that acceleration acts towards the centre of mass of the Sun.
Then this needs to be multiplied by a unit vector that is perpendicular to the velocity. There may be easier or better ways to do this, but my solution involved geometry. I calculated the angle of the velocity vector using \(\tan\theta = \left(\frac{v_x}{v_y}\right)\) and I set the unit acceleration vector to \(a=\,<\cos\theta,\sin\theta,0>\).
My issue is that there has to be a better method of producing a centre-seeking force. I would prefer to define a central point and have a force vector directed at that point. After all, planets do not orbit because their acceleration is perpendicular to their velocity, but because the force that causes that acceleration acts towards the centre of mass of the Sun.