Warwick Long Bay, Bermuda. Waves coming ashore on a breezy day. The colours have not been enhanced, Bermuda really is this beautiful! (Photo: Kate Kayaian)
|
Sound >>
|
10.1 - Waves on a String
Objectives:
- To understand how transverse waves move along a string.
- To know what happens when two waves moving in opposite direction meet.
- To know the factors that affect the speed of a wave on a string
- To understand that standing waves (harmonics) can form on a string fixed between two points and use this to measure the speed of the wave.
- To be able to derive and apply the cello equation
|
Waves are the periodic disturbance of a medium. They can transfer both energy and information. We experience waves every day: sound, light, microwaves for our phones and internet, to the waves that we experience off South Shore due to the weather!
Photo: My wife, Kate, is a professional cellist. Therefore, I have started to learn far more about the science of music than I ever thought necessary! 
|
Relection and Superposition
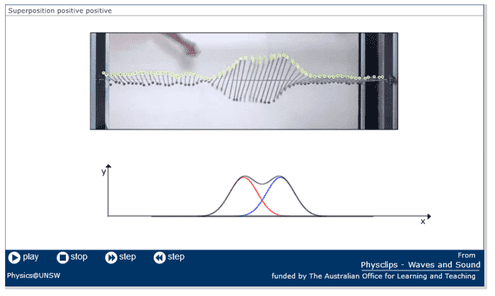
When two waves meet, they do not change, except for the short period when they coincide. After they have passed each other they carry on going their own way, as if they had never met. Click the image below to view two of the excellent PhysClips animations. PhysClips is a very useful website that has been created by the University of New South Wales in Australia. Their wave animations are probably the best that I have seen in terms of clarity. It is well worth looking around and running all of them.
When two waves meet, they do not change, except for the short period when they coincide. After they have passed each other they carry on going their own way, as if they had never met. Click the image below to view two of the excellent PhysClips animations. PhysClips is a very useful website that has been created by the University of New South Wales in Australia. Their wave animations are probably the best that I have seen in terms of clarity. It is well worth looking around and running all of them.
Image still from the animation from PhysClips to show how the phase of the reflected pulse depends on whether the end is free or fixed.
|
Image still from the animation from PhysClips that shows the superposition of two wave pulses.
|
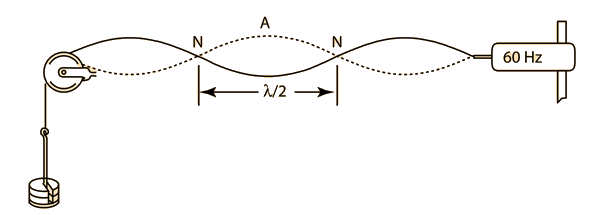
Waves on a String
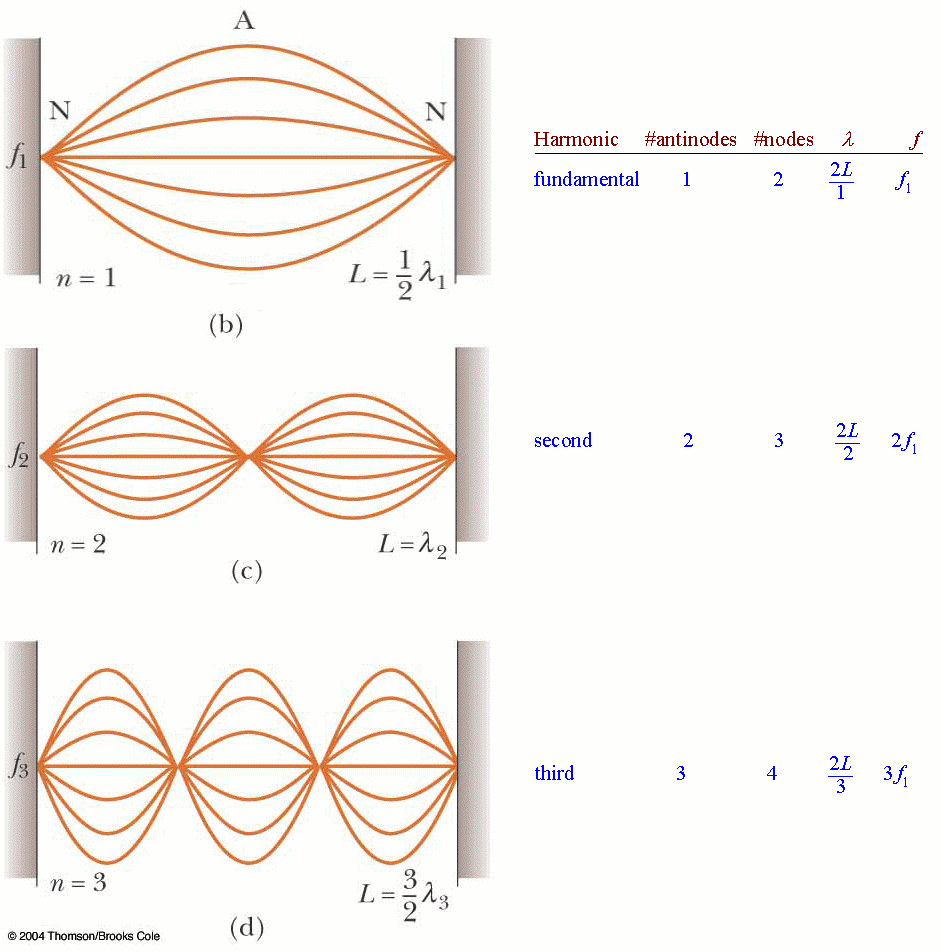
A taut string can be vibrated by plucking it (guitar), bowing it (cello) or setting up a vibration generator at the end (physics). This is usually connected to a signal generator which can vary the frequency and the amplitude of the vibration. If the frequency of the wave is just right, then the reflected waves from the ends return in phase with the incoming wave to produce standing waves. This effect is also called resonance. The different frequencies that this effect occurs at depends on how the wavelength matches the length of the string and are called the harmonics. The lowest frequency that exists is called the first or fundamental harmonic, and the subsequent ones are the second, third and fourth harmonics. The variables that can change the frequency of the harmonics are:
A taut string can be vibrated by plucking it (guitar), bowing it (cello) or setting up a vibration generator at the end (physics). This is usually connected to a signal generator which can vary the frequency and the amplitude of the vibration. If the frequency of the wave is just right, then the reflected waves from the ends return in phase with the incoming wave to produce standing waves. This effect is also called resonance. The different frequencies that this effect occurs at depends on how the wavelength matches the length of the string and are called the harmonics. The lowest frequency that exists is called the first or fundamental harmonic, and the subsequent ones are the second, third and fourth harmonics. The variables that can change the frequency of the harmonics are:
- tension of the string
- mass per unit length of the string
- length of the string
|
|
We take the wave equation that links the speed, wavelength and frequency of the wave:
\[v=f\lambda\]
and the equation that governs the speed of the wave on a string - which is based on the tension of the string and its resistance to moving.
\[v = \sqrt{\frac{T}{\mu }}\]
to get the equation that governs the note that a stringed instrument produces!
\[f = \frac{1}{\lambda }\sqrt{\frac{T}{\mu }}\]
\[v=f\lambda\]
and the equation that governs the speed of the wave on a string - which is based on the tension of the string and its resistance to moving.
\[v = \sqrt{\frac{T}{\mu }}\]
to get the equation that governs the note that a stringed instrument produces!
\[f = \frac{1}{\lambda }\sqrt{\frac{T}{\mu }}\]
|
|
|
|
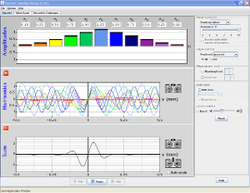
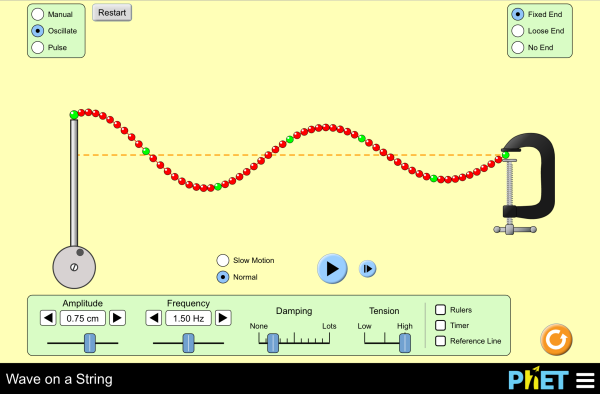
PhET Simulation - new version! It is good to try to see how standing waves are formed. Start off by seeing what happens to a pulse that reflects off a) a fixed end and b) a free end point. Then try to alter the frequency of the oscillator to set up a stable standing wave. There is a lag in the wave simulation, so be a little patient.
|
|
Physics Aviary Virtual Lab - this is a simulation of the actual lab that we will be performing. I call this experiment the "physics of a cello", as we can demonstrate the equation that governs the note produced by a stringed instrument.
|
Sound >>
Other Resources
