Crossfire off South Shore - BOCA race 2015. Yacht navigation requires a good understanding of velocity, distance and time.
|
Dynamics >>
|
1.5 - Two Dimensional Motion
Objectives:
- To know that the time-of-flight for a projectile is the same as it would be if the object had no horizontal motion
- To be able to break motion at an angle into two perpendicular components
- To be able to add two vectors together
- To be able to use the above and trigonometry to solve simple projectile problems.
This is where the fun really starts! So far, we have only considered one-dimensional motion. But in everyday life we have two and three-dimensional motion all the time. At AP level we only consider two-dimensions, but you could extend this to three-dimensions using the same basic ideas. The standard scenario for this sort of work at AP is projectile motion (ballistics).
KEY CONCEPT: Vectors that are perpendicular to each other can be treated independently. Time is the linking variable.
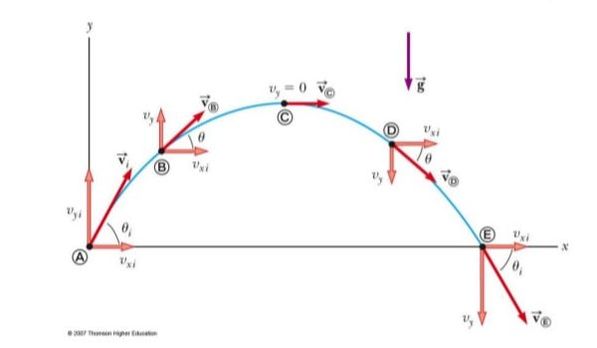
The image above shows a ball following a parabolic ballistic trajectory. Consider both the vertical and horizontal motions.
Vertical: The ball decelerates on the way upwards to a stop at the apex and then accelerates downwards again. The acceleration is \(g\).
Horizontal: The ball is moving at a constant speed as evinced by the equal spacing of the lines.
The time of flight is the same - the ball only moves sideways for as long as it is in the air. The time is also symmetrical. The time up = time down.
(Note: air resistance is always neglected in these situations.)
You will be performing a number of lab experiments on this topic.
Historical trivia: this is one of the things that made mechanics respectable in the early days! Once physicists could accurately predict the range of a cannonball, lords and kings started to take notice.
Vertical: The ball decelerates on the way upwards to a stop at the apex and then accelerates downwards again. The acceleration is \(g\).
Horizontal: The ball is moving at a constant speed as evinced by the equal spacing of the lines.
The time of flight is the same - the ball only moves sideways for as long as it is in the air. The time is also symmetrical. The time up = time down.
(Note: air resistance is always neglected in these situations.)
You will be performing a number of lab experiments on this topic.
Historical trivia: this is one of the things that made mechanics respectable in the early days! Once physicists could accurately predict the range of a cannonball, lords and kings started to take notice.
|
Example 1
The simplest problem is the most common and involves firing a projectile horizontally from a height. The initial vertical velocity is zero and the initial horizontal velocity is the launch speed, \(v\). Step 1 - calculate the time-of-flight from the vertical motion. \[x = v_{o}t +\frac{1}{2}at^{2}\] as initial vertical speed is zero and acceleration is \(g\), this becomes: \[t=\sqrt{\frac{2h}{g}}\] Step 2 - calculate the range from the horizontal motion. \[x = vt=v\sqrt{\frac{2h}{g}}\] |
|
Example 2
If the ball is thrown upwards at angle (as shown above) - then we need split the velocity into vertical and horizontal components before we do any physics. This is where sines and cosines come in: \[v_{x}=v\cos \theta\] \[v_{y}=v\sin \theta\] Looking carefully at the diagram you should be able to see that the horizontal velocity vector is constant, while the vertical one changes continuously. The actual speed of the ball can be found by applying Pythagoras's Theorem. |
So, the first step in determining the range of the projectile is to find out the time-of-flight. This is done by finding how long it takes to go up and fall back down again. We usually know three variables: the initial vertical speed, the acceleration (gravity) and the final vertical speed. So, using the first of the kinematic equations gives us:
\[a = \frac{\Delta v}{t}\]
\[t=\frac{\Delta v }{a}=\frac{v\sin \theta }{g}\]
This is the time to go up. The total time-of-flight is double this, so we have:
\[t=\frac{2v\sin \theta }{g}\]
\[a = \frac{\Delta v}{t}\]
\[t=\frac{\Delta v }{a}=\frac{v\sin \theta }{g}\]
This is the time to go up. The total time-of-flight is double this, so we have:
\[t=\frac{2v\sin \theta }{g}\]
Step 2: Consider the horizontal motion. The ball is traveling at a constant speed of the horizontal component of the initial speed, \(v_x\) .
\[x = vt=v_{x}t=v\cos \theta \cdot \frac{2v\sin \theta }{g}\]
With a bit of tidying up becomes:
\[x = \frac{2v^{2}\sin \theta \cos \theta }{g}\]
\[x = vt=v_{x}t=v\cos \theta \cdot \frac{2v\sin \theta }{g}\]
With a bit of tidying up becomes:
\[x = \frac{2v^{2}\sin \theta \cos \theta }{g}\]
|
Example 3
This is the most challenging of all the situations and requires all of the above and dividing the flight into two distinct sections: up and down. It is above the standard required for AP - however, you may be asked to either a) describe the effects of raising or lowering the launch height or b) changing the angle of the launch. Anyway, the range is below. Advanced students can see if they can derive it! \[x = v\cos \theta \left ( \frac{v\sin \theta }{g}+\sqrt{\frac{2h}{g}} \right )\] These screenshots from projectiles lab work carried out 22 Oct by AP Physics 1 class using the VideoPhysics app on an iPad. As can be seen on the left, it is not always sunny in Bermuda! |
Challenge: Can you solve the problem set by Peter's teacher?
|
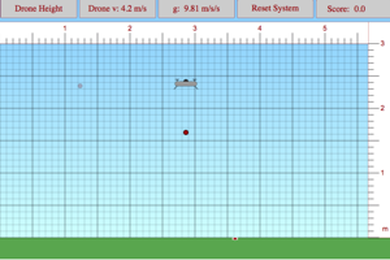
Physics Aviary Game: Drone Delivery Challenge. The idea to drop packages from a moving drone onto a target - Amazon Prime??
|
ACTIVITY
Use the PhysGL software to produce an animation of
Use the PhysGL software to produce an animation of
- a projectile being thrown up into the air at an angle.
- a projectile moving along a table and falling to the ground
- a projectile being launched off a ramp.
- Use a light gate to determine the velocity of a steel ball launched from a spring-loaded launcher. Then mount the launcher on a surface and use the data to predict where the ball will hit the floor. Place a 'pancake' of plasticene on the floor and fire your projectile. What is your accuracy? What could be a potential source of error.
- BONUS - set the launcher up at an angle and repeat the above exercise!
ASSIGNMENTS
| cw_1.6_projectile_calculations.pdf | |
| File Size: | 109 kb |
| File Type: | |
| cw_1.7_phet_projectiles_lab.pdf | |
| File Size: | 254 kb |
| File Type: | |
| hw_1.5_horizontal_projectiles.pdf | |
| File Size: | 126 kb |
| File Type: | |
Newton's Laws >>
Other Resources
|
Bozeman Science - Motion This is an excellent video that describes position, velocity and acceleration
|
|
Motion Graphs - interactive graphing
|
Wonders of Physics - Kinematics. Excellent cartoons from Evan Toh
|
CK12 Physics - Motion - great site loaded with videos
Interactive projectiles simulation - fun one with sound effects!
|
|
Tracker - a computer based version of the VideoPhysics app. A bit more flexible than the app and more accurate as you can import a video from a higher quality camera than the iPad has. The mouse pointer is easier to use! The video tutorial is a bit of a must.
|