Bermuda Motorcross Racing (Photo: Takara Dill)
6.1 - Linear Momentum and Impulse
- To be able to calculate the momentum of a moving object.
- To understand that a force is required to change an object's momentum.
- To know that the impulse the product of the force and time and is equal to the change of momentum.
The momentum of a moving object is simply the product of its mass and its velocity. It is a vector quantity. Its usefulness lies in the fact that it is conserved during a collision (or explosion). It is a more complete description of the property of a moving object as the mass is included. So far we have assumed that Newton's Laws are for objects that have a constant mass, but mass can and does change.
Newton's First Law in momentum terms is that if there is no net external force then the momentum of a system will not change.
Newton's Second Law states that the force required to change the velocity of an object is the product of its \(mass \times acceleration\). The underlying assumption is that the mass is constant and only the velocity changes. A more correct version is that the force required is equal to the rate of change of momentum:
\[F=\frac{\Delta p}{t}\]
If this is rearranged to put the change of momentum on one side, we are left with the product of \(force\times time\). This is called the IMPULSE of the force. It is numerically equal to the change of momentum. If the force varies as a function of time, the impulse is equal to the area under the F-t graph.
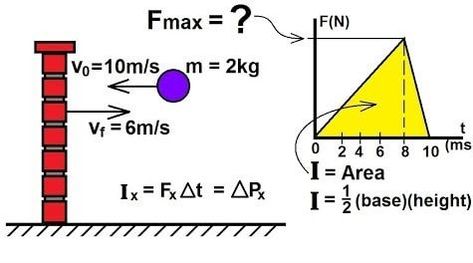
Note that the momentum is a vector quantity. If the direction changes, the momentum changes as well. The most common example of that is when a ball bounces off a wall. Let's say that a ball of mass \(2.0 \,\text{kg}\) hits a wall at \(10.0 \,\text{m/s}\) and rebounds at \(6.0 \,\text{m/s}\). The impulse and change of momentum is:
Newton's First Law in momentum terms is that if there is no net external force then the momentum of a system will not change.
Newton's Second Law states that the force required to change the velocity of an object is the product of its \(mass \times acceleration\). The underlying assumption is that the mass is constant and only the velocity changes. A more correct version is that the force required is equal to the rate of change of momentum:
\[F=\frac{\Delta p}{t}\]
If this is rearranged to put the change of momentum on one side, we are left with the product of \(force\times time\). This is called the IMPULSE of the force. It is numerically equal to the change of momentum. If the force varies as a function of time, the impulse is equal to the area under the F-t graph.
Note that the momentum is a vector quantity. If the direction changes, the momentum changes as well. The most common example of that is when a ball bounces off a wall. Let's say that a ball of mass \(2.0 \,\text{kg}\) hits a wall at \(10.0 \,\text{m/s}\) and rebounds at \(6.0 \,\text{m/s}\). The impulse and change of momentum is:
|
\[Ft=\Delta p= 2\,\text{kg}\times \left ( 10 \,\text{m/s} - -6\text{m/s}\right ) = 32 \,\text{kgm/s}\]
Notice that in this example, this impulse is also equal to the area shaded in yellow as the force is not constant with time. If we could measure the maximum force of the impact we could determine how long it took and vice versa. |
Other Resources
PhET SImulation: Collision Lab