|
Projectiles >>
|
1.4 - Problem Solving Tips
Objectives:
- To understand the importance of visualising the problem before starting to try to solve it
- To be able to draw an accurate, labelled diagram
- To be able to convert units before attempting to solve a problem.
Without a shadow of a doubt, the hardest aspect for any student at this level is how solve a physics problem! IGCSE Physics was easy, just learn an equation, rearrange it and stick the numbers in. Bish. Bash. Bosh. Done. Most students find the concepts and equations of kinematics easy to learn - after all there are only THREE of them - but suddenly the questions become nightmarishly difficult. What is the speed that an apple passes a window in the French class when it thrown upwards at \(3 \,\text{m/s}\) from the top of the piazza? How soon after it was thrown does another student need to throw another apple upwards from the field at the same speed for the apples to collide in full view of the students in that class?
If two events are occurring at the same point in time, they are happening SIMULTANEOUSLY. Therefore we need to solve two equations simultaneously. So, finally, this is the real purpose for those simultaneous equation questions that your Maths teacher kept making you do.
The hard part is not the maths, it is how to figure out how even begin to tackle the problem and many students starting out get stuck. From years of experience I can safely state that THIS IS NORMAL. You are not alone!
Unfortunately, while it is possible to make students aware of techniques and patterns, problem solving itself cannot be taught. It is a skill that has to be learned. And this takes time and practice. Arguing about the problem in small groups often helps.
There are many techniques to problem solving. A well-tested method that I start with, and STRONGLY ENCOURAGE, is to draw a well-labeled diagram of the problem, with everything that you know (or want to know) marked on it. This is the beginning of a process that we call MODELLING, and that is a highly transferable skill that is used in science, engineering, maths, weather and climate, finance and insurance. This is the reason that physics is such a highly valued subject. It is not important that you know the date that Newton figured out gravity or whether you can recite Ohm's Law - what matters is that you can consider a problem and figure out how to solve it logically.
If two events are occurring at the same point in time, they are happening SIMULTANEOUSLY. Therefore we need to solve two equations simultaneously. So, finally, this is the real purpose for those simultaneous equation questions that your Maths teacher kept making you do.
The hard part is not the maths, it is how to figure out how even begin to tackle the problem and many students starting out get stuck. From years of experience I can safely state that THIS IS NORMAL. You are not alone!
Unfortunately, while it is possible to make students aware of techniques and patterns, problem solving itself cannot be taught. It is a skill that has to be learned. And this takes time and practice. Arguing about the problem in small groups often helps.
There are many techniques to problem solving. A well-tested method that I start with, and STRONGLY ENCOURAGE, is to draw a well-labeled diagram of the problem, with everything that you know (or want to know) marked on it. This is the beginning of a process that we call MODELLING, and that is a highly transferable skill that is used in science, engineering, maths, weather and climate, finance and insurance. This is the reason that physics is such a highly valued subject. It is not important that you know the date that Newton figured out gravity or whether you can recite Ohm's Law - what matters is that you can consider a problem and figure out how to solve it logically.
|
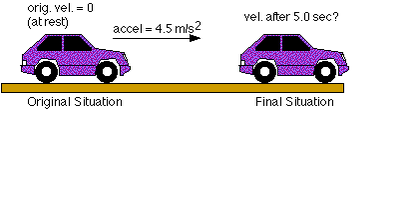
An example of a well-labelled diagram for a kinematics problem. Note that all the known variables are clearly shown, as it what the unknown variable that we are trying to find (the velocity after 5 seconds. You could also label the time as \(t = 5\,\text{s}\) between the pictures of the cars. Top Tip: make your diagrams large enough that you can add to them afterwards if you need to.
|
ASSIGNMENT
- below is an example of an old AP problem that involves changes of motion, so is not simply a case of plugging in numbers into an equation, rather it requires a bit of logic and breaking the motion into sections.
| cw_1.5_past_ap_question.pdf | |
| File Size: | 200 kb |
| File Type: | |