Hurricane Irma from space (September 2017)
|
Home >> AP Physics I >> Rotational Mechanics >> Rotational Dynamics
|
7.3 - Rotational Dynamics
- To know that a torque is required to change the rate of rotation of an object.
- To understand the concept of rotational inertia (moment of inertia) as the resistance to change of rotation of an object.
- To know the rotational inertias of simple objects (disk, hoop, bar, solid and hollow spheres.)
- To know, understand and use Newton's First and Second Laws in the context of rotation.
- To be able to draw a free body diagram of a rolling object.
Rotational Inertia
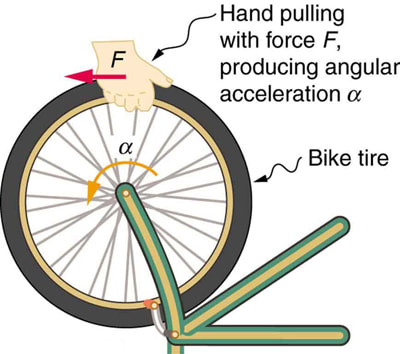
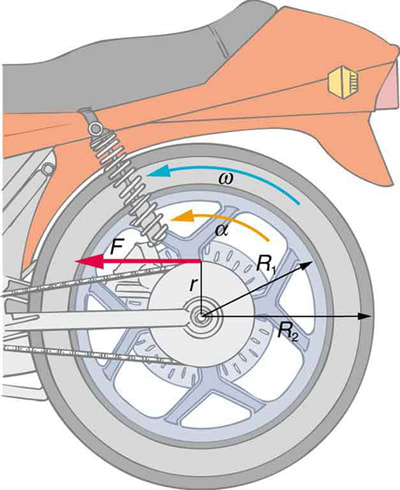
Now for the hardest concept: In order to change the rotation of an object you require a torque - this is simply the tangential force applied x the radial distance of the force. But the object will resist the change in motion, much the same way that any object resists a change in linear motion. In the linear case this resistance to motion is due to the mass or inertia of the object. For rotating bodies, this inertial property is called the rotational inertia (or moment of inertia). The larger the rotational inertia the harder it is to change the speed rotation. Mathematically the rotational inertia is defined as the required torque/(change in angular velocity), much the same way as mass = required force/acceleration for linear motion. Newton's first and second law still apply. In the absence of a resistive torque a spinning object will continue to spin forever. The Earth being an excellent example!
The rotational inertia of object is a function of their geometry. Mathematically it is always a function of *mr2 (coefficient x mass x radius squared). The coefficient can be determined by considering where the centre of mass of a radial section is. If the centre of mass is at the rim them I = mr2. If it is half way to the rim then I = 1/2mr2. Objects with the mass towards the rim are harder to change the rotation of than objects with the mass concentrated towards the centre.
\[I = (coeff)mr^{2}\]
Now for the hardest concept: In order to change the rotation of an object you require a torque - this is simply the tangential force applied x the radial distance of the force. But the object will resist the change in motion, much the same way that any object resists a change in linear motion. In the linear case this resistance to motion is due to the mass or inertia of the object. For rotating bodies, this inertial property is called the rotational inertia (or moment of inertia). The larger the rotational inertia the harder it is to change the speed rotation. Mathematically the rotational inertia is defined as the required torque/(change in angular velocity), much the same way as mass = required force/acceleration for linear motion. Newton's first and second law still apply. In the absence of a resistive torque a spinning object will continue to spin forever. The Earth being an excellent example!
The rotational inertia of object is a function of their geometry. Mathematically it is always a function of *mr2 (coefficient x mass x radius squared). The coefficient can be determined by considering where the centre of mass of a radial section is. If the centre of mass is at the rim them I = mr2. If it is half way to the rim then I = 1/2mr2. Objects with the mass towards the rim are harder to change the rotation of than objects with the mass concentrated towards the centre.
\[I = (coeff)mr^{2}\]
|
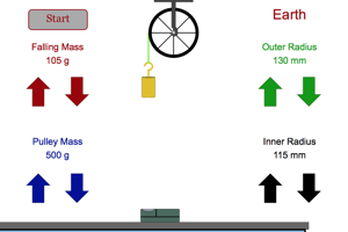
Physics Aviary - Virtual Lab
This is a simulation of the real lab that we do in class, although we can't change the goemetry of the wheel as this one can do. Variables include the mass of the pulley and the suspended object as well as the inner and outer radius of the pulley. The most interesting is changing from a hoop to a disk, but keeping the masses the same. The moment of interia of a disk is half of that of a hoop of the same radius and mass. (Another great HTML V simulation from Frank McCulley.) |
|
|
LAB WORK: Jordan uses a descending mass to rotate a T-bar with some hanging masses.
|
Other Resources
|
|
|