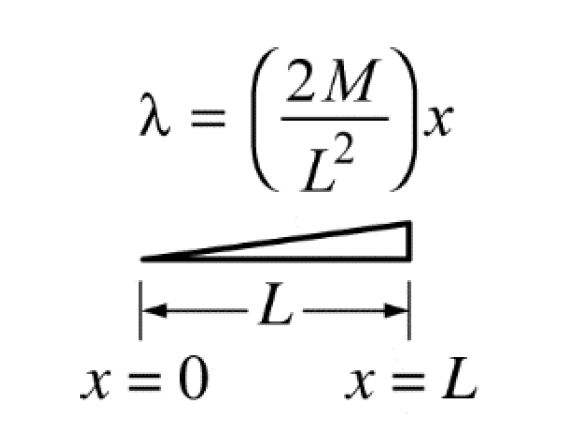Every so often some of our students decide to take the AP Physics C (Mechanics) exam. If the student has done well in AP Physics I and is taking AP Calculus, then it is perfectly possible to get an excellent grade in the exam without much extra knowledge, but it does require practicing the past questions a lot as they are quite different to the new style Physics I. Personally I prefer them. It should be mentioned that calculus itself only applies to a few parts of a question, but the trick is to understand what it means and when to apply it.
The format of the exam is that there are three questions, equally weighted. The third question is always a rotational mechanics question that has a reputation for being a toughie.
The format of the exam is that there are three questions, equally weighted. The third question is always a rotational mechanics question that has a reputation for being a toughie.
What is Calculus?
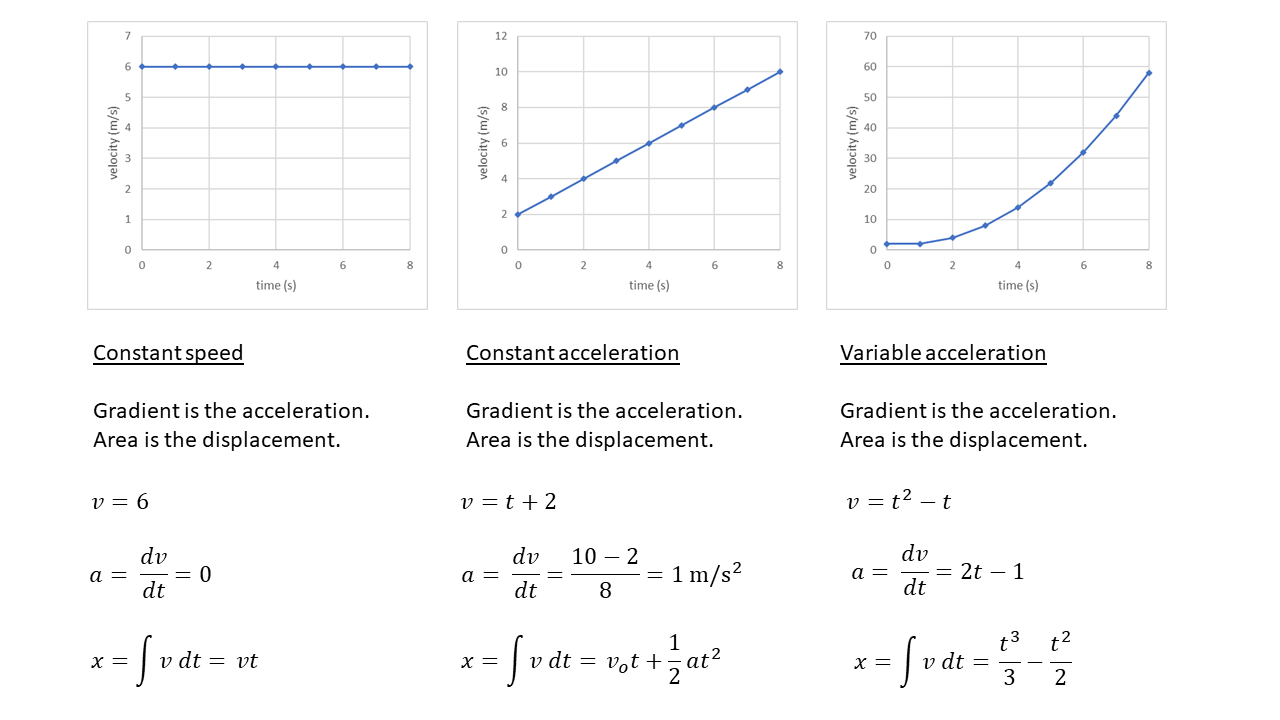
What is calculus? Simply put it is the technique to deal with variables that are changing, usually with time. Essentially, it relates gradients and areas under graphs. Working on the assumption that the basics are well understood, I will just apply to mechanics. Here is an example using velocity-time graphs:
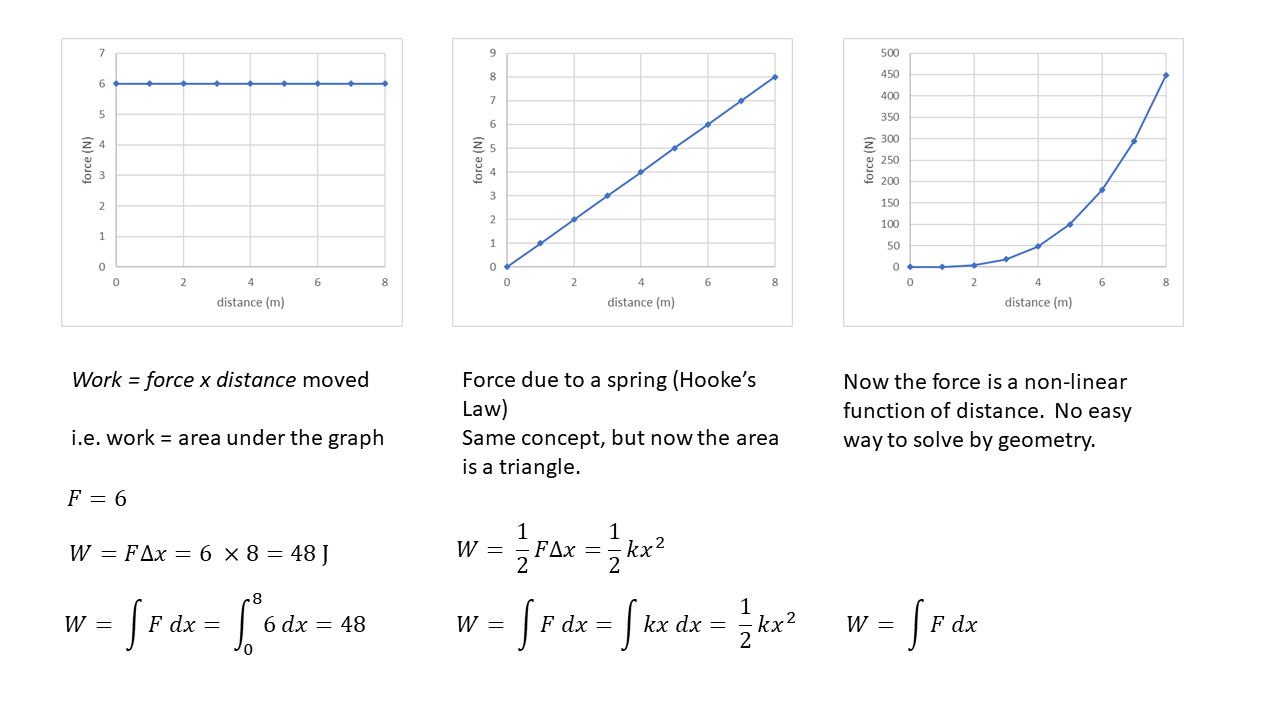
So, any variable that can be determined by the area of a graph means that it is the integral of that variable. The three classics are: kinematic displacement (see above) \(v\left(t\right)\), impulse \(F\left(t\right)\) and work \(F\left(x\right)\) .
Simple Harmonic Motion
Simple harmonic motion (SHM) is dealt with in more detail for AP-C. Usually in the context of springs. The period and frequency stay the same from AP-1, but the kinematics is more rigorous.
The fundamental principle of SHM is that it matches uniform circular motion (see AP-1/8). Given that it begins with an initial displacement, it must follow a cosine wave. The \(\left(\omega t\right) \) part relates to the frequency. If the angular velocity \(\omega\) was a full circle it would equal \(\frac{2\pi}{T}\), so would reduce to \(2\pi\). The cosine of \(2\pi=1\). The particle has returned to its original location. (see angular velocity AP-1 Unit 7)
\[x=\cos{(\omega t)}\]
The fundamental principle of SHM is that it matches uniform circular motion (see AP-1/8). Given that it begins with an initial displacement, it must follow a cosine wave. The \(\left(\omega t\right) \) part relates to the frequency. If the angular velocity \(\omega\) was a full circle it would equal \(\frac{2\pi}{T}\), so would reduce to \(2\pi\). The cosine of \(2\pi=1\). The particle has returned to its original location. (see angular velocity AP-1 Unit 7)
\[x=\cos{(\omega t)}\]
The velocity is the derivative:
\[v=\frac{dx}{dt}=-\omega\sin{(\omega t)}\]
\[v=\frac{dx}{dt}=-\omega\sin{(\omega t)}\]
The acceleration is the second derivative:
\[a=\frac{d^2x}{dt^2}=-\omega^2\cos{(\omega t)}\]
\[a=\frac{d^2x}{dt^2}=-\omega^2\cos{(\omega t)}\]
which further reduces to:
\[a=-\omega^2\;x\]
\[a=-\omega^2\;x\]
which is actually the more correct definition of SHM - the acceleration is proportional to the negative of the displacement. In AP-1 we covered the graphical version of this qualitatively with the gradients representing the velocity and accelerations.
Non-SHM
If the spring does not 'obey' Hooke's Law, i.e. that the force is NOT proportional to the extension, then the oscillator does not perform SHM, but rather a more complex motion. To work out the speed at any given point in the oscillation you would have to revert to the conservation of energy:
If the spring does not 'obey' Hooke's Law, i.e. that the force is NOT proportional to the extension, then the oscillator does not perform SHM, but rather a more complex motion. To work out the speed at any given point in the oscillation you would have to revert to the conservation of energy:
\[ EPE = KE \]
BUT remembering that the EPE is not \(\frac{1}{2}\;kx^{2}\) but rather the integral of the force as a function of displacement. Needless to say, the period would not be the same as a simple harmonic oscillator. You would not be expected to calculate that.
Rotational Mechanics
One of the three questions on the AP-C exam will be rotational mechanics. The difference between AP-1 and AP-C is probably the greatest for this topic in term of how they structure the question. In AP-1 it usually involves a single object, while in AP-C it frequently involves more than one and the questions are more mathematical in nature. Ensure that the work in AP-1 Unit 7 is fully understood first!
Determining the Moment of Inertia for a Compound Object
This is pretty straightforward - just add them together. For example, if a blob of plasticine of mass m is sitting at the edge of a disk of mass M and radius R, we get:
\[I_{disk}=\frac{1}{2}MR^{2}\]
\[I_{blob}=mR^{2}\]
\[I_{total}=\left ( \frac{M}{2}+m\right )R^{2}\]
This is pretty straightforward - just add them together. For example, if a blob of plasticine of mass m is sitting at the edge of a disk of mass M and radius R, we get:
\[I_{disk}=\frac{1}{2}MR^{2}\]
\[I_{blob}=mR^{2}\]
\[I_{total}=\left ( \frac{M}{2}+m\right )R^{2}\]
What if the axis is not at the centre of mass?
Here we can use a brilliant result known as the "parallel axis theorem". As Mr Viotti says, "it is amazing because just add \(mx^{2}\) on to it". The derivation for this can be looked up online or in a physics book, but essentially he is correct, you take the moment of inertia of the object with the axis being the centre of mass as normal and add the moment of inertia of the centre of mass based on the new axis.
For example: a disk of mass \(M\) and radius \(R\), but pivoted at the rim rather than the centre. (more lie it flops than it actually rotates!)
Here we can use a brilliant result known as the "parallel axis theorem". As Mr Viotti says, "it is amazing because just add \(mx^{2}\) on to it". The derivation for this can be looked up online or in a physics book, but essentially he is correct, you take the moment of inertia of the object with the axis being the centre of mass as normal and add the moment of inertia of the centre of mass based on the new axis.
For example: a disk of mass \(M\) and radius \(R\), but pivoted at the rim rather than the centre. (more lie it flops than it actually rotates!)
|
Moment of inertia of the disk through its centre of mass:
\[I_{disk}=\frac{1}{2} MR^{2}\] Switching the position of the axis to a distance x from the centre of mass: \[I_{new}=\frac{1}{2}MR^{2} +Mx^{2}\] but as the distance in this case is x = R, we get: \[I_{new}=\frac{3}{2}MR^{2}\] |
Using Calculus to Derive the Moment of Inertia.
This can be tricky, but luckily the AP-C question always seems to give you the answer, so bottom line is that you can skip this, do the rest of the question to maximise your score, then come back to it if you have the time.
The definition of the moment of inertia is the sum of the components of the mass multiplied by the square of the radial distance from the pivot.
\[I=\sum m_{i}r_{i}^{2}\]
which, when transformed into a continuous sum, becomes:
\[I=\int_{0}^{R} r^{2} dm\]
But this is impractical to use as we want to integrate over distance, not mass...
The key is to determine the ratio of how the mass varies with length, i.e. \( \frac{dm}{dr}\), which is often called \(\lambda.\)
If the object is linear - for example a rod, beam or stick of mass \(M\) and length \(L\), then the ratio is also linear. If pivoted at the end we get:
\[\lambda=\frac{dm}{dr}=\frac{M}{L}\]
A quick bit of algebra to get \(dm\) on the left hand side gives us:
\[dm=\frac{M}{L} dr\]
This can then be switched into the integral by replacing the \(dm\) part with the \(dr\) bit:
\[ I=\frac{M}{L} \int_{0}^{L} r^{2} dr=\frac{M}{L} \left[ \frac{r^{3}}{3} \right]_{0}^{L}\]
which yields:
\[I=\frac{ML^{3}}{3L}\]
\[I=\frac{ML^2}{3}\]
This can be tricky, but luckily the AP-C question always seems to give you the answer, so bottom line is that you can skip this, do the rest of the question to maximise your score, then come back to it if you have the time.
The definition of the moment of inertia is the sum of the components of the mass multiplied by the square of the radial distance from the pivot.
\[I=\sum m_{i}r_{i}^{2}\]
which, when transformed into a continuous sum, becomes:
\[I=\int_{0}^{R} r^{2} dm\]
But this is impractical to use as we want to integrate over distance, not mass...
The key is to determine the ratio of how the mass varies with length, i.e. \( \frac{dm}{dr}\), which is often called \(\lambda.\)
If the object is linear - for example a rod, beam or stick of mass \(M\) and length \(L\), then the ratio is also linear. If pivoted at the end we get:
\[\lambda=\frac{dm}{dr}=\frac{M}{L}\]
A quick bit of algebra to get \(dm\) on the left hand side gives us:
\[dm=\frac{M}{L} dr\]
This can then be switched into the integral by replacing the \(dm\) part with the \(dr\) bit:
\[ I=\frac{M}{L} \int_{0}^{L} r^{2} dr=\frac{M}{L} \left[ \frac{r^{3}}{3} \right]_{0}^{L}\]
which yields:
\[I=\frac{ML^{3}}{3L}\]
\[I=\frac{ML^2}{3}\]
A More Complicated Example
This was found on the 2018 AP-C exam paper. The answer is stated to be \(I=\frac{ML^{2}}{2}\). The task is to prove it.
This was found on the 2018 AP-C exam paper. The answer is stated to be \(I=\frac{ML^{2}}{2}\). The task is to prove it.
|
It is super important is to remember that \(\lambda=\frac{dm}{dx}\) and that \(x\) is the variable rather than \(r\).
\[\lambda=\frac{dm}{dx} = \left (\frac{2M}{L^{2}}\right )x\] \[ dm = \left(\frac{2M}{L^{2}} \right) x\; dx \] Then using the integral definition of moment of inertia, remembering to rename the variables: \[I=\int_{0}^{L} x^{2} dm\] substituting in the \(dx\) part for the \(dm\) bit: \[I=\int_{0}^{L} x^{2} \left (\frac{2M}{L^{2}}\right )x\;dx\] Removing constants from the integral and tidying up: \[ I=\left (\frac{2M}{L^{2}}\right )\int_{0}^{L} x^{3} \;dx\] \[ I=\left (\frac{2M}{L^{2}}\right )\left[\frac{x^{4}}{4}\right ]_{0}^{L} \] \[ I=\left (\frac{2M}{L^{2}}\right )\left[\frac{L^{4}}{4}\right ] \] \[I=\frac{ML^{2}}{2}\]
|
This problem then continued to use these wedges as the spokes of a wheel and the task was to determine the overall moment of inertia of the wheel.
|
\[ I_{total}=\sum I_{i}\]
\[I_{total}=I_{hoop}+3I_{wedge}\] \[I_{total}=mR^{2}+3\left(\frac{MR^{2}}{2}\right)\] In this question, conveniently the mass of the hoop is the same as the masses of each of the spokes: \[I_{total}=\frac{5}{2}MR^{2}\] |
Useful reference: Physics LibreTexts