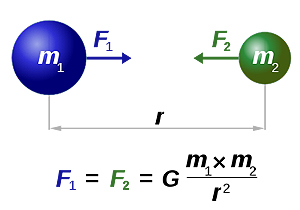|
Orbits >>
|
3.3 - Newton's Law of Gravitation
Objectives:
- To understand the Law of Gravitation
- To be able to calculate the force between any two objects
- To understand the nature of the inverse square law
- To understand the concepts of weight and mass
- To be able to calculate the weight of an object
- To understand the concept of gravitational field strength
The basic physics: any two masses attract each other with a force that depends on the product of their mass and is inversely proportional to the distance that separates them. The constant of proportionality, known as the Universal Gravitational Constant, \(G\):
\[G = 6.67 \times 10^{-11}\,\text{Nm}^{2}\text{kg}^{-2}\]
\[G = 6.67 \times 10^{-11}\,\text{Nm}^{2}\text{kg}^{-2}\]
This was first successfully measured by Cavendish in 1798. The experiment was quite something. He suspended two large balls on a lightweight beam suspended by a thin wire. A mirror mounted on the wire reflected a beam of sunlight focused upon it. He then raised two other balls to be close to the first balls. The tiny force of gravity was enough to provide a torque and rotate the balls together by a few degrees. This movement of the wire caused by this deflection would amplified by the beam bouncing off the mirror. By varying the separation of the balls, Cavendish obtained enough data to establish a good estimate for the value of the Gravitational Constant. As the mathematics of orbital mechanics had by this time been worked out, in effect he had measured the masses of the Earth and Sun!
So, why the inverse square law?
So, why the inverse square law?
|
|
|
Weight and Gravitational Field Strength
WEIGHT is the name given to the force that gravity pulls down on a specific object. The amount of 'stuff' in the object itself is called MASS. Mass can also be thought of its 'resistance' to a change in motion or its inertia. We usually denote weight by \(mg\). At the surface which is most of the time in physics problems(!), we tend to assume that has a fixed value of \(g = 9.81 \,\text{m/s}^2\) and think of it as the acceleration due to gravity. Actually it is the gravitational field strength, or how much force the Earth pulls on each kilogram of mass. Its units are \(\text{N/kg}\). In the absence of air resistance, a falling object accelerates at the same rate as the gravitational field strength. This is not a coincidence but rather a direct consequence of Newton's 2nd Law.
\[a=\frac{F}{m}\]
\[a=\frac{mg}{m}\]
\[a=g\]
\[a=\frac{F}{m}\]
\[a=\frac{mg}{m}\]
\[a=g\]
Another way to think of this is that mass does not change depending where you travel too, but the weight due to gravity does. An object in space may be weightless, but it still has mass. Kicking it will still hurt.
The gravitational field strength, g, varies as the force acting on an object varies. It is defined as the force due to gravity per kilogram of mass:
\[g = \frac{F}{m}\]
\[g = \frac{GM}{r^{2}}\]
The gravitational field strength, g, varies as the force acting on an object varies. It is defined as the force due to gravity per kilogram of mass:
\[g = \frac{F}{m}\]
\[g = \frac{GM}{r^{2}}\]
Substituting the known values for the radius of the Earth, the mass of the Earth and the Universal Gravitational Constant yields the expected value of \(g = 9.81 \,\text{N/kg}\) . The gravitational field strength varies from location to location and from planet to planet. Students often believe that gravity 'stops' in space, i.e. outside the atmosphere as they see astronauts floating in the ISS. Adding the space station's altitude of \(400 \,\text{km}\) to the radius results in a tiny reduction in the gravitational field strength.
Example 1 - The Force between the Earth and an Apple
The force due to gravity effectively acts from the centre of mass. The mass of the Earth is \(6.0 \times 10^{24}\,\text{kg}\) and its radius is \(6370\,\text{km}\). If the mass of an apple is \(0.1 \,\text{kg}\), then the force of gravity on the apple is:
\[F=\frac{GMm}{r^2}\]
\[F = \frac{(6.67\times10^{-11} \times 6.0\times10^{24} \times 0.1)}{(6.37\times10^{6})^2}\]
\[F = 1.0\,\text{N}\]
This is its weight! Now, surprisingly, this is the same force that the apple exerts on the Earth. The forces are mutual and so equal and opposite. So, does the Earth move? Not much. Say that the apple takes \(1.5\,\text{s}\) to fall to the ground.
\[a=\frac{\sum{F}}{m}\]
\[a = \frac{1.0}{6.0\times 10^{24}}\]
\[a = 1.7 \times 10^{-25}\,\text{m/s}^2\]
then distance moved is found using kinematics;
\[x = v_ot+\frac{1}{2}at^2\]
\[x = \frac{1}{2} \times 1.7 \times 10^{-25} \times (1.5)^2 \]
\[x = 1.0\times10^{-25}\,\text{m}\]
This is a ten-billionth the radius of a proton. So, not far. A more interesting calculation would be to measure the distance moved if everyone in China jumped up at the same time!
The force due to gravity effectively acts from the centre of mass. The mass of the Earth is \(6.0 \times 10^{24}\,\text{kg}\) and its radius is \(6370\,\text{km}\). If the mass of an apple is \(0.1 \,\text{kg}\), then the force of gravity on the apple is:
\[F=\frac{GMm}{r^2}\]
\[F = \frac{(6.67\times10^{-11} \times 6.0\times10^{24} \times 0.1)}{(6.37\times10^{6})^2}\]
\[F = 1.0\,\text{N}\]
This is its weight! Now, surprisingly, this is the same force that the apple exerts on the Earth. The forces are mutual and so equal and opposite. So, does the Earth move? Not much. Say that the apple takes \(1.5\,\text{s}\) to fall to the ground.
\[a=\frac{\sum{F}}{m}\]
\[a = \frac{1.0}{6.0\times 10^{24}}\]
\[a = 1.7 \times 10^{-25}\,\text{m/s}^2\]
then distance moved is found using kinematics;
\[x = v_ot+\frac{1}{2}at^2\]
\[x = \frac{1}{2} \times 1.7 \times 10^{-25} \times (1.5)^2 \]
\[x = 1.0\times10^{-25}\,\text{m}\]
This is a ten-billionth the radius of a proton. So, not far. A more interesting calculation would be to measure the distance moved if everyone in China jumped up at the same time!
Example 2- Another Planet's Gravity MC Questions
A very common AP question is to compare the gravity of Earth to that of another that has (say) twice the mass and twice the radius of the Earth. A good technique is to use altered variables denoted by a prime, '. Note that \( G \) is universal and does not need to be changed.
\[g{}' = \frac{GM{}'}{r{}'^{2}}\]
\[g{}' = \frac{GM{}'}{r{}'^{2}}\]
Then substitute the changed values: \(M{}' = 2M\) (twice the mass of Earth) and \(r{}' = 2r\) (twice the radius of Earth). Note that I have used brackets to reduce potential errors!
\[g{}' =\frac{G(2M)}{\left ( 2r \right )^{2}}=\frac{2GM}{4r^{2}}\]
\[g{}' =\frac{G(2M)}{\left ( 2r \right )^{2}}=\frac{2GM}{4r^{2}}\]
As we know that \(\frac{GM}{r^2} = g_{Earth}\), this simplifies down to half that of Earth's:
\[g{}'=\frac{2GM}{4r^{2}}=\frac{2}{4}\left ( \frac{GM}{r^{2}} \right )=\frac{g}{2}\]
\[g{}' =\frac{g}{2}\]
\[g{}'=\frac{2GM}{4r^{2}}=\frac{2}{4}\left ( \frac{GM}{r^{2}} \right )=\frac{g}{2}\]
\[g{}' =\frac{g}{2}\]
Other Resources
|
|
|