Bermuda Motorcross Racing (Photo: Takara Dill)
6.2 - Conservation of Momentum
- To understand that in the absence of an external force, the total momentum of a system is conserved.
- To know that this is a consequence of Newton's First Law of Motion
In any closed system, if there is no external force acting on it, the overall momentum is conserved. This is a direct consequence of Newton's First Law of Motion. I will discuss what a closed system is later - it is a key concept at AP. Generally the law of conservation of momentum is used for collisions and explosions. Drawing a pair of well-labelled diagrams to show the 'before' and 'after' situation of the event is extremely useful and is actively encouraged.
Collisions
There are a couple of common situations: an object runs into another head on a collide or it bounces off. Note the before and after on all of the diagrams!
Collisions
There are a couple of common situations: an object runs into another head on a collide or it bounces off. Note the before and after on all of the diagrams!
|
|
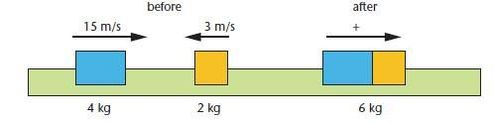
The overall momentum before the collision is the sum of the two momenta, with the \(2 \,\text{kg}\) cart being negative as it is moving to the left.
\[p_{before}= p_{1}+p_{2}= \left ( 4\times 15 \right )+\left ( 2\times -3 \right )=54\, \text{kgm/s}\] Therefore, the total momentum of the coupled carts after must also equal \(56 \,\text{kgm/s}\). \[p_{after}= 54 \,\text{kgm/s}= (6\, \text{kg}\times v)\] \[v = \frac{54}{6}=9 \,\text{m/s}\] |
The interesting thing about the above example is that if you think about it really carefully you can see that the centre of mass of the system continues to move at a constant speed to the right. This is Newton's First Law. Our previous version of it assumed that we were dealing with ONE object whose mass is constant. But really we should consider a more general version of it.
In the absence of an external resultant force the motion of a closed system remains constant. The motion is defined by momentum as it involves not only the velocity but the mass as well. The situation above is such a closed system. Now if an external force such as friction or due to a gradient was involved the momentum would not be conserved. We analyse it further by saying that the centre of mass will accelerate. But that is beyond the scope of this sub-topic.
In the absence of an external resultant force the motion of a closed system remains constant. The motion is defined by momentum as it involves not only the velocity but the mass as well. The situation above is such a closed system. Now if an external force such as friction or due to a gradient was involved the momentum would not be conserved. We analyse it further by saying that the centre of mass will accelerate. But that is beyond the scope of this sub-topic.
Experimental work
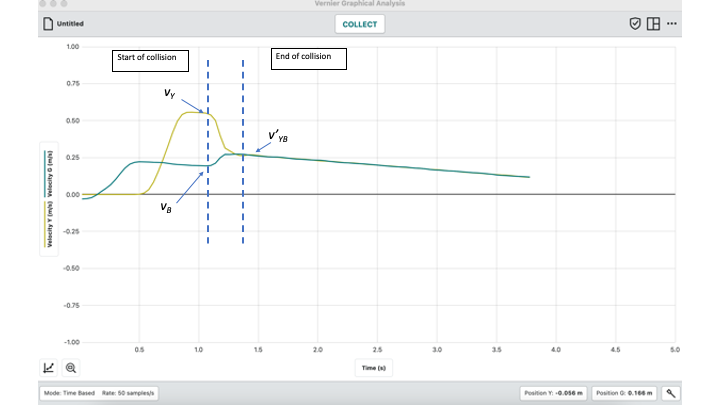
With motion sensors built into low friction carts, it is now possible to carefully analyse real collisions and explosions and verify the law of conservation of momentum. The first experiment was using velcro pads to enable the carts to stick together in a totally inelastic collision (i.e. KE is not conserved, but a large percentage is lost to heat during the collision).
With motion sensors built into low friction carts, it is now possible to carefully analyse real collisions and explosions and verify the law of conservation of momentum. The first experiment was using velcro pads to enable the carts to stick together in a totally inelastic collision (i.e. KE is not conserved, but a large percentage is lost to heat during the collision).
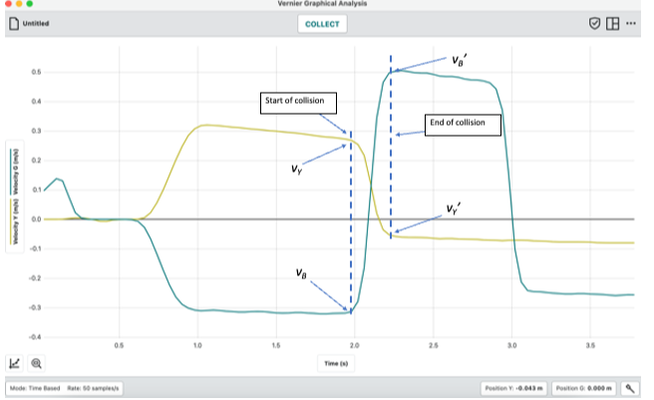
The graph below represents the data from a nearly perfectly elastic collision that was achieved by using neodynium magnets mounted on the two carts. The yellow cart was laden with extra masses and the two carts had a head on collision. The yellow cart recoiled backwards at a slow rate, while the blue one had a more dramatic recoil due to its smaller mass.
Other Resources
PhET SImulation: Collision Lab