|
Dynamics >>
|
2.2 - Static Equilibrium (Statics)
Objectives:
- To understand that in order for an object to remain stationary or moving at a constant velocity the forces must balance
- To be able to solve static problems using either geometry or maths
Since middle school we have discussed balanced forces. Now we are going to look at them in more detail. This is the major application of the first law. If the forces are balanced then the motion does not change - it either remains at rest or continues to move at a constant velocity. The latter is important to remember! Usually statics problems involves things that do NOT move. Engineering and architecture is heavily influenced by statics. After all, if your structure does not remain stationary when you want it to, things go badly for you....
Mathematically the statement for saying that all the forces are balanced is: \[\sum{F}=0\]
However is it more useful to express it like this:\[F\uparrow =F\downarrow\] \[F\leftarrow\: = F\rightarrow\]
Mathematically the statement for saying that all the forces are balanced is: \[\sum{F}=0\]
However is it more useful to express it like this:\[F\uparrow =F\downarrow\] \[F\leftarrow\: = F\rightarrow\]
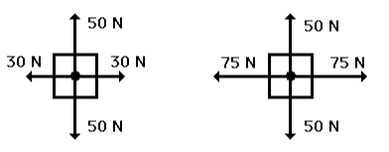
Remember from kinematics that vectors at right angles to each other can be considered independent. This concept gets used a huge amount in physics --> see the home page for just one example! The diagram below shows a couple of simple examples. As the forces are balanced in the opposite directions, the objects are in equilibrium. Note that it is impossible from the diagram to tell whether they are stationary or in motion. (Geek moment: this eventually leads into Einstein's Theory of Special Relativity....)
So, this seems way too simple for AP Physics..... Well, the forces are not always nicely lined up and perpendicular with other, so we frequently have to break one or more of the forces into components using trigonometry and/or Pythagoras. Often it is convenient to change our definition of UP and DOWN to make the maths easier.
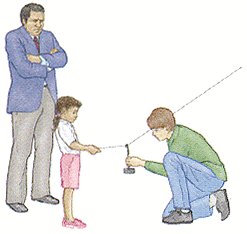
Example 1 - Kite String
|
|
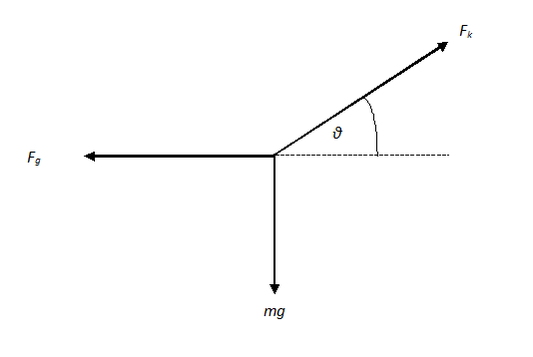
The picture above shows a set up to measure the tension in a kite string. The judge measures the angle shown and the weight added to the string. He then uses the concept of statics to work out the tension in the string. \[F\uparrow=F\downarrow\] \[F_{k}\sin \theta =mg\] \[F_{k}=\frac{mg}{\sin \theta }\]
Note that in this case we do not need to consider the horizontal forces to solve the problem. However, we could determine that the pulling force on the girl's hand is: \[F\leftarrow\:=F\rightarrow\] \[F_{g}=F_{k}\cos \theta\]
Example 2 - The Classic Block-on-a-Slope
In the classic physics 'block-on-slope' problems, it is usually easier to define UP as perpendicular to the slope. It is not 100% essential, but it does make the mathematics a great deal easier!
|
Forces perpendicular to the slope are the Normal, \(N\), and the perpendicular component of the weight. \[F\uparrow=F\downarrow\] \[N=mg\cos \theta\]
Now for the forces parallel to the slope which are the slopewards component of the weight and the force of friction, \(f\). \[F\leftarrow=F\rightarrow\] \[mg\sin \theta =f\]
We now have two simultaneous equations to solve, depending on what variables were given in the problem.
|
Tasks - Online Statics Challenges
|
|
|
|
Fun photo that is going around the internet at the moment. Not sure of the original source. But anyhoo.... Explain how this works. You are allowed to use equations, diagrams and values should you wish. This could be the next AP-1 exam question.
|
COVER PHOTO - Bermuda fitted dinghies racing in Granaway Deep. (Photo: Tom Clarke)
Dynamics >>
Other Resources
Newton's Laws and Car Crashes - recommended by Morgan Kornarski of Safe Kids
|