Hurricane Irma from space (September 2017)
7.2 - Rotational Kinematics
Objectives:
- To be able to measure the rate of rotation of a spinning object in the lab.
- To be able to quantify the rate of rotation of a spinning object by any of the following variables: period, frequency, angular velocity, tangential velocity.
- To be able to switch fluently between these four variables.
Rotational motion is slightly harder to conceptualise than linear motion. The key as far as I am concerned is to fully understand the variables that describe the rotation of an object. The easiest of these is the frequency, how many times the object rotates in \(1 \,\text{s}\). In reality, the timescale of seconds is often replaced by minutes. Therefore the frequency is quantified by the number of rotations per minute (rpm). This is often seen on bikes (e.g. a pedal bike may rotate at \(70 \,\text{rpm}\), and a motorbike engine at \(2500 \,\text{rpm}\) ). As with other applications, the period is the reciprocal of the frequency.
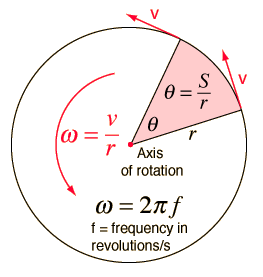
The tangential velocity is the same as with circular motion, and calculate by \(speed = distance\, \text{/}\,time =circumference\,\text{/}\, time\). The tangential velocity decreases as the radius of the object decreases. In theory, the very centre of the axle is not moving! The final key variable for basic rotation is the angular velocity. This is the rate of change of angle. The simplest was to calculate this is \(\frac{360^{\circ}}{period}\). This will yield an angular velocity in degrees per second. In the more useful units of radians:
The tangential velocity is the same as with circular motion, and calculate by \(speed = distance\, \text{/}\,time =circumference\,\text{/}\, time\). The tangential velocity decreases as the radius of the object decreases. In theory, the very centre of the axle is not moving! The final key variable for basic rotation is the angular velocity. This is the rate of change of angle. The simplest was to calculate this is \(\frac{360^{\circ}}{period}\). This will yield an angular velocity in degrees per second. In the more useful units of radians:
|
Clocks
The clock on the left is on Reid Street, Hamilton. On the right is Big Ben on the Houses of Parliament, London. The angular velocities of the minute and hour hands of every clock in the world are the same. i.e. The minute hand sweeps through \(360^{\circ}\) in one hour everywhere. However, the tip of the minute hand of Big Ben moves faster than that of the Reid Street clock as its radius length is far greater. |
If you are comfortable with these variables and with chopping and changing between them, that is half the battle with this unit.
The equations below are the LINKING equations between linear and rotational variables. You just need to learn one of these and the others follow the same pattern. As an aide memoire I use the middle one and check whether the velocity tends to zero as the radius tends to zero to check I have the right way around...
They follow the pattern: \(linear\, variable= radius \times rotational\, variable\)
\[s=r\theta\]
\[v=r\omega\]
\[a=r\alpha\]
The equations below are the LINKING equations between linear and rotational variables. You just need to learn one of these and the others follow the same pattern. As an aide memoire I use the middle one and check whether the velocity tends to zero as the radius tends to zero to check I have the right way around...
They follow the pattern: \(linear\, variable= radius \times rotational\, variable\)
\[s=r\theta\]
\[v=r\omega\]
\[a=r\alpha\]
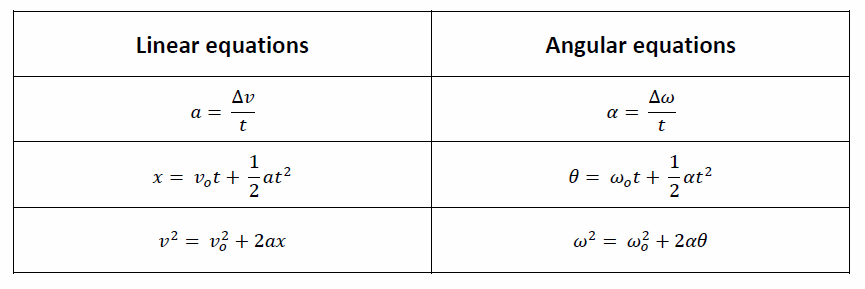
The kinematics equations are practically the same as the three that you learned from Unit 1 - Kinematics. We have simply replaced the linear variable with its rotational equivalent. (angle for displacement, angular velocity for velocity and angular acceleration for acceleration). They can be converted back and forth using the linking equations above. You will be measuring these in the lab and performing numerous calculations.
Gibb's Hill Lighthouse
The lighthouse appears to have a flashing light on the top. In reality it is a fixed light and a revolving set of five lenses. The lenses sit on a mercury bearing, which famously become inoperative after Hurricane Fabian in 2003. Originally the rotation was powered by a system of gears that were powered by a torque provided by a \(1200 \,\text{lb}\) mass that ran through the centre of the lighthouse. This had to be re-hoisted to the top of the lighthouse every \(5 \,\text{hours}\)! These days, an electric motor under a plywood box causes the rotation of the beams.
Data: On a humid night it is possible to see the 5 beams of light rotating out from the lantern. The period of rotation was measured as \(45\,\text{s}\). What is the angular velocity and what is the flash rate of the lighthouse as seen from a ship? What would be the tangential speed of the beams some \(26 \,\text{km}\) out to sea? From the video, can you estimate the angular velocity of the radar?
The lighthouse appears to have a flashing light on the top. In reality it is a fixed light and a revolving set of five lenses. The lenses sit on a mercury bearing, which famously become inoperative after Hurricane Fabian in 2003. Originally the rotation was powered by a system of gears that were powered by a torque provided by a \(1200 \,\text{lb}\) mass that ran through the centre of the lighthouse. This had to be re-hoisted to the top of the lighthouse every \(5 \,\text{hours}\)! These days, an electric motor under a plywood box causes the rotation of the beams.
Data: On a humid night it is possible to see the 5 beams of light rotating out from the lantern. The period of rotation was measured as \(45\,\text{s}\). What is the angular velocity and what is the flash rate of the lighthouse as seen from a ship? What would be the tangential speed of the beams some \(26 \,\text{km}\) out to sea? From the video, can you estimate the angular velocity of the radar?
|
A cloudy winter's day in Bermuda! Left, Gibb's Hill lighthouse and above, the original mechanism that converted the linear motion of the descending mass to the rotational motion of the lenses. In the foreground, the shaft and dog clutch for the modern electric motor can be seen. The bevelled gear serves no purpose now. There would have been a winding handle for the keeper to winch up the driving mass.
|
|
|
Video of the radar at the top of the lighthouse. This and another one at Fort George can fix the position of every ship around the island.
|
\[v=r\omega\] As the radius increases, the tangential (linear) velocity increases.
Other Resources
|
YouTube clip - rigid body rotation lecture
|