Photo: a diver exploring the wreck of the Marie Celestia. (credit: Dive Bermuda)
|
The waters surrounding Bermuda are stunning. They are warm, blue, clear and teaming with life. The colours are amazing and the diving is amongst the best in the world. The reefs that encircle the island are littered with shipwrecks. Every Bermudian should spend serious time in the sea during the summer!
The Biostation in Bermuda has just started working with underwater gliders - the future of oceanography. These work by changing the buoyancy of the nose cone to allow them to dive to up to \(1000\,\text{m}\) depth, before changing the buoyancy again to rise back to the surface. As they sink/rise at an angle, the water flowing over the wings produces lift (the Bernoulli Effect) that is translated into forward motion through the ocean. The hulls are carbon fibre, as they have to be strong enough to withstand the huge pressures at those depths. |
|
11.1 - Hydrostatic Pressure
Objectives:
- To know how to measure and/or calculate the density of matter
- To understand the concept of pressure and use the equation \(P = \frac{F}{A}\)
- To be able to calculate the hydrostatic pressure at any given depth.
- To know the difference between gauge pressure and absolute pressure.
Hydrostatic pressure is simply the pressure of a fluid due to the weight of the fluid above it.
|
If you are underwater, either snorkling or diving, you feel an added pressure around you due to the weight of the water above you. This pressure is exerted almost evenly all over your body. (Almost, as you have a non-zero vertical dimension). This even distribution is known as Pascal's Principle. The pressure due to the weight of the water above you is known as Hydrostatic Pressure (pressure due to stationary water). Of course, this fluid does not need to be water, but the name has stuck. The classic spouting can experiment (left) clearly shows that the deeper the hole, the faster the water comes out as it is at a higher pressure.
|
|
The "gauge" pressure or pressure difference at any given depth depends on only three variables: density of the fluid, depth and the gravitational field strength. If there is a pressure above the surface of the fluid, which could be due to either the weight of the atmosphere (atmospheric pressure) or another force, then this must be added to the gauge pressure to produce the "absolute pressure".
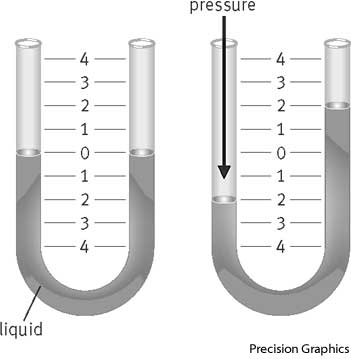
The simplest possible pressure gauge is the manometer. This is a straightforward U-tube filled with a liquid. When both ends are exposed to the same pressure, in this case atmospheric pressure, then the fluid levels are equal. If one side is exposed to a higher pressure, then the levels are not equal. The difference in heights lead directly to the pressure difference or gauge pressure. |
|
\[\Delta P = \rho g\Delta h\]
This equation is one that you have met before. It comes from \(P = \frac{F}{A}\), where the \(F = mg\) of the water and the mass = density x volume = density x depth x area. The area terms cancel out leaving Pressure difference = density x g x depth. If the external pressure due to the atmosphere is included we get an expression for the absolute pressure: \[P = P_{o}+\Delta P\]
The units of pressure are many and varied. The SI unit is newtons/square metre, which is called Pascals (Pa) in honour of Blaise Pascal. If pressure differences are being considered, then pretty much any unit will do, including the imperial unit that is common in Bermuda, psi (pounds per square inch or \(\text{lb/in}^2\). Meteorologists use millibars. 1 millibar = 100 Pa.
This equation is one that you have met before. It comes from \(P = \frac{F}{A}\), where the \(F = mg\) of the water and the mass = density x volume = density x depth x area. The area terms cancel out leaving Pressure difference = density x g x depth. If the external pressure due to the atmosphere is included we get an expression for the absolute pressure: \[P = P_{o}+\Delta P\]
The units of pressure are many and varied. The SI unit is newtons/square metre, which is called Pascals (Pa) in honour of Blaise Pascal. If pressure differences are being considered, then pretty much any unit will do, including the imperial unit that is common in Bermuda, psi (pounds per square inch or \(\text{lb/in}^2\). Meteorologists use millibars. 1 millibar = 100 Pa.
|
Example: a scuba diver exploring the wreck of the Hermes is at a depth of \(24\,\text{m}\) below the surface of the ocean. The density of seawater is \(1030\,\text{kg/m}^3\) and the atmospheric pressure is \(101 \,\text{kPa}\).
\[\Delta P=\rho gh\] \[\Delta P=1030 \times 10 \times 24 = 2.47\times 10^{5} \, \text{Pa}\] The absolute pressure needs to include the atmosphere pressure of 101 kPa \[P = 1.01 \times 10^{5}+2.47\times 10^{5} \, \text{Pa}\] \[P = 3.48\times10^{5}\,\text{Pa}\] which is about 3.4 atm (atmospheres). As a diver's rule of thumb the pressure increases by about 1 atm for every 10 m (30 ') descended. |
|
Whenever I went to Boston I would see this 'Wizard's Tower' on the skyline. So, I cycled up the hill that it was on and went to see if the wizard was home. Turns out that it is a thin type of water tower called a standpipe. It provides water pressure to the surrounding area. Pumps lift water to the top and the standpipe regulates and evens out the water pressure. Some architect decided to make it look all fancy! Normally in the US, water towers are large and ugly looking mushrooms.
|
11.2 - Archimedes' Principle
Objectives:
- To understand what causes the upthrust and to be able to calculate it in a wide range of situations.
- To be able to calculate the waterline of a floating object.
Archimedes' Principle is probably the oldest law of physics there is. All the other natural 'laws' figured out by the ancients have not stood the test of time, but this one has! Being based on an island, we spend a lot of time in and on the ocean, so it is an important one to become well versed in. It can get quite mathematical too, which is cool!
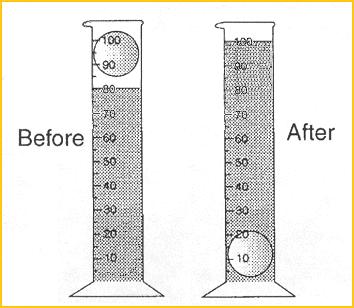
The basic concept famously discovered by Archimedes while in his bathtub was that an object displaces its own submerged volume of water. With hindsight this is blindingly obvious... As an object is submerged into the water, the water that was where the object is must go somewhere else after all. The bird in one of Aesop's Fables knew this as he dropped stones into a narrow hollow so as to raise the water level enough that he could drink.
A really useful exercise is to use a variety of regular shapes and a measuring cylinder to show that their volumetric equations are correct. E.g. the volume of a sphere is determined by:
The basic concept famously discovered by Archimedes while in his bathtub was that an object displaces its own submerged volume of water. With hindsight this is blindingly obvious... As an object is submerged into the water, the water that was where the object is must go somewhere else after all. The bird in one of Aesop's Fables knew this as he dropped stones into a narrow hollow so as to raise the water level enough that he could drink.
A really useful exercise is to use a variety of regular shapes and a measuring cylinder to show that their volumetric equations are correct. E.g. the volume of a sphere is determined by:
|
\[V = \frac{4}{3}\pi r^{3}\]
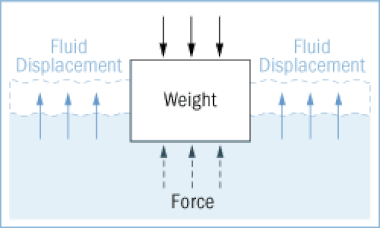
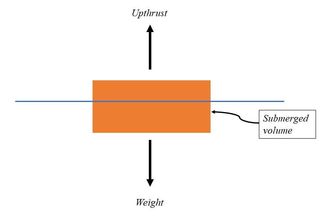
So, drop a ball into a beaker of water and measure the 'apparent' change of volume. It should be exactly the same value. Of course, this is NOT how the equations were derived, but it is somewhat reassuring that mathematical theory matches empirical reality! However, this displaced volume is not Archimedes' Principle. It is that this displaced volume of water causes an upwards force on the object displacing it. He figured out that the upwards force of buoyancy is exactly equal to the weight of the water displaced. The greater the volume of displaced water, the greater the buoyant force (often called "upthrust"). To fully appreciate how the volume affects the buoyancy of an object try submerging a) a tennis ball and b) a beach ball... |
|
Bermuda's tall ship is the "Spirit of Bermuda". She floats because the upthrust from the displaced water from her underwater volume is identically equal to her weight. If her weight increases, then the weight is greater than the upthrust and she sits lower in the water until the increased displacement once again balances her weight.
"Spirit" was built out of wood in Maine based on a design of a "Ballyhoo schooner" found on a painting in the National Maritime Museum of London, which shows one of the easiest examples of the now ubiquitous Bermuda rig (triangular sails). The original Bermuda Sloops were considered too unsafe to replicate. The project was the brainchild of Malcolm Kirkland. More info: Bermuda Sloop Foundation |
|
So what causes this force of buoyancy? There are two easy ways to look at it:
a) It is due to the hydrostatic pressure caused by the depth of the submerged object spread over the area. Every object has a depth to it. Very thin objects have very little buoyancy. b) the water displaced upwards by the object is trying to return to where it came from as water always runs downhill due to gravity. To get a sense for this, go to the beach with a spoon and start frantically digging a hole in the ocean... |
Mathematics
There are generally two types of problem that involve Archimedes' Principle and they are dependent on whether the object is totally submerged or floating on the surface. Submerged is the easiest. Assume that the fluid involved is water for simplicity.
1 - Submerged
There are two ways that an object can remain submerged, a) it is denser than the water and has sunk or b) it is buoyant but held below the surface by a mooring rope. Either way the weight of the object is simply \(mg\), and the buoyant upthrust is the weight of the water displaced, which is equal to the \(water\,density \times volume\,displaced \times g\). The volume of water displaced for a submerged object is identically equal to the volume of the object.
\[F_{B}=\rho_{water} V_{water}g\]
For objects that are held down, simply use Newton's 1st Law to realise that the forces up must balance the forces down and calculate either the tension in the rope.
Example: A cork of mass \(10\,\text {g}\) and density \(250 \,\text{kg/m}^3\) is held under the surface of water by a length of cotton string. What is the tension in the string?
There are generally two types of problem that involve Archimedes' Principle and they are dependent on whether the object is totally submerged or floating on the surface. Submerged is the easiest. Assume that the fluid involved is water for simplicity.
1 - Submerged
There are two ways that an object can remain submerged, a) it is denser than the water and has sunk or b) it is buoyant but held below the surface by a mooring rope. Either way the weight of the object is simply \(mg\), and the buoyant upthrust is the weight of the water displaced, which is equal to the \(water\,density \times volume\,displaced \times g\). The volume of water displaced for a submerged object is identically equal to the volume of the object.
\[F_{B}=\rho_{water} V_{water}g\]
For objects that are held down, simply use Newton's 1st Law to realise that the forces up must balance the forces down and calculate either the tension in the rope.
Example: A cork of mass \(10\,\text {g}\) and density \(250 \,\text{kg/m}^3\) is held under the surface of water by a length of cotton string. What is the tension in the string?
|
\[F\uparrow =F\downarrow\]
\[F_{B} = mg+T\] \[\rho Vg = mg+T\] The volume of the cork can be determined from its mass and density \(V=\frac{m}{\rho}\). The classic error here is to get mixed up with the density of the object and the density of the fluid. Density of water = \(1000\,\text{kg/m}^3\). \[T = \rho Vg - mg = \left ( 1000\times \left ( 0.01/250 \right ) \times 10\right )-\left ( 0.01\times10 \right )\] \[T = 0.3\; \text{N}\] |
2 - Floating
The maths of a floating object is slightly harder as the volume of water displaced is less than the volume of the object. Usual questions on this tend to be how much of the object is submerged and how much extra weight on top would cause it to sink. As the floating object is in equilibrium, we can state that the forces up = forces down, and so the upthrust must be equal to the weight.
The maths of a floating object is slightly harder as the volume of water displaced is less than the volume of the object. Usual questions on this tend to be how much of the object is submerged and how much extra weight on top would cause it to sink. As the floating object is in equilibrium, we can state that the forces up = forces down, and so the upthrust must be equal to the weight.
|
\[F_{B}= mg\]
Substituting in and taking care with the two different VOLUMES and DENSITIES leads to: \[\rho_{fluid} g V_{submerged}= mg = \rho_{object} g V_{object}\] \[\rho_{fluid} V_{submerged}= \rho_{object} V_{object}\] |
Then, the depth of the object that is submerged can be determined from remembering that the volume = area x height. (Of course, this assumes that the object has a regular shape such as a raft.) To obtain the maximum mass that the raft can handle, just set the submerged volume equal to the volume of the object itself.
Puzzles
|
|
Physics Girl YouTube Video - this is a classic physics puzzle about Archimedes' Principle. If you sit in a boat in a small pond and throw a rock or anchor overboard, does the water level rise, fall or stay the same?
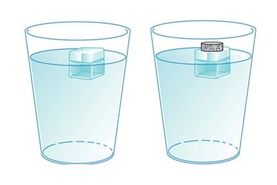
Below - two identical glasses of water with identical cubes of ice floating in them. One has a coin sat on top. What happens to the water levels in the glasses when the ice melts and why? 
|
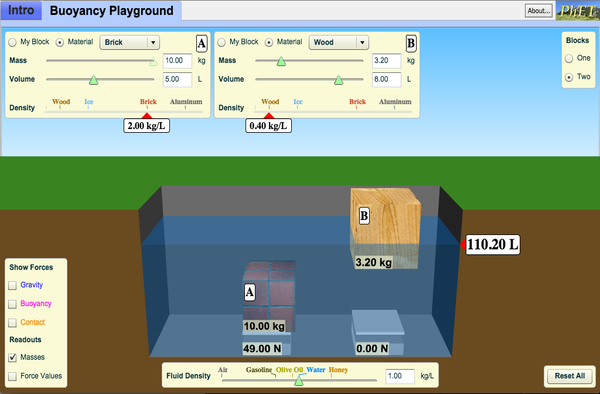
Some PhET simulations that you can play with:
|
|
11.3 - Fluid Flow
Objectives:
- To be able to use the principle of continuity to calculate the speed of a fluid flowing through a pipe.
So far we have discussed stationary or static fluids. However, interesting things happen when fluids move. This happens all the time. Fluids move in the ocean and atmosphere, inside bike engines and plumbing, over the wings of aircraft, the blades of a propeller, and over the sails and foils of a sailing boat.
|
Both gases and liquids are considered to be fluids, in that they can flow. In this section we will look at the relationships between fluid flowing in regular and irregular manners and how the motion of the fluid affects the pressure of the fluid.
We can understand many behaviours of a fluid by considering an ideal set of conditions:
|
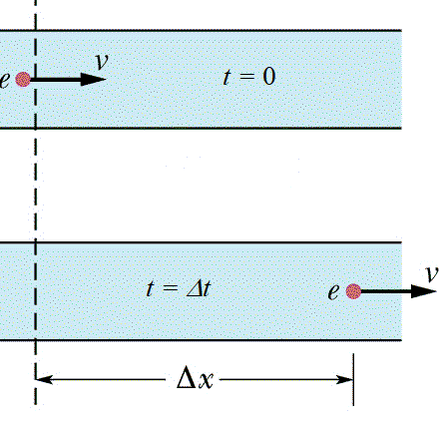
Consider a fluid moving through a tube as shown in the diagram, During a given time period \(\Delta t\) a volume \(\Delta V\) passes through the tube. The flow rate, \(f\), is the volume of fluid that flows through per second – i.e. \(f=\frac{\Delta V}{\Delta t}\) .
During this small time interval, \(\Delta t\), the fluid travels a distance \(\Delta x\). The velocity of the fluid is \(v\), which is equal to \(\frac{\Delta x}{\Delta t}\).
Given that the volume is equal to the cross-sectional-area multiplied by a given length \(\Delta x\) we can change the flow rate equation into a new form.
\[f=\frac{\Delta V}{\Delta t}\]
\[f=\frac{A \Delta x}{\Delta t}= A v\]
During this small time interval, \(\Delta t\), the fluid travels a distance \(\Delta x\). The velocity of the fluid is \(v\), which is equal to \(\frac{\Delta x}{\Delta t}\).
Given that the volume is equal to the cross-sectional-area multiplied by a given length \(\Delta x\) we can change the flow rate equation into a new form.
\[f=\frac{\Delta V}{\Delta t}\]
\[f=\frac{A \Delta x}{\Delta t}= A v\]
|
So, based on the principle that the rate of flow of volume must stay constant throughout a pipe (or other system), then changing the cross-sectional area must change the speed of the fluid.
Note: this is not just true for fluids, but also traffic! Home experiment: take a hose pipe and squeeze the end to reduce the cross-sectional area. What do you notice about the speed that the water comes out? |
|
The diagram shows a constriction in a pipe that carries a moving fluid. Where the pipe narrows, the fluid flows faster. This type of system is known as Venturi and is important in engineering.
\[f = v_{1}A_{1}=v_{2}A_{2}\] |
|
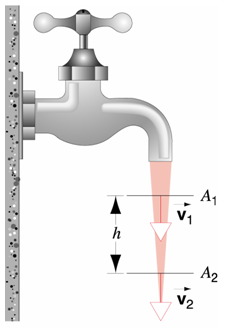
If you open a tap and adjust so that the water is smoothly flowing in such a way that there is no sign of turbulence, you will notice that the diameter of the stream narrows as it moves away from the tap. This is due to the water accelerating due to gravity. As the speed increases the cross-sectional area decreases as the water molecules are bound together.
|
11.4 - Torricelli's Theorem
Objectives:
- To verify by investigation that the speed that the water comes out of a tank depends on the depth of the water above the opening.
- To be able to use this relationship to calculate the range of a jet of water.
- To understand that increasing the pressure above the liquid, increases the speed of the jet.
- \(v = \sqrt{2gh}\)
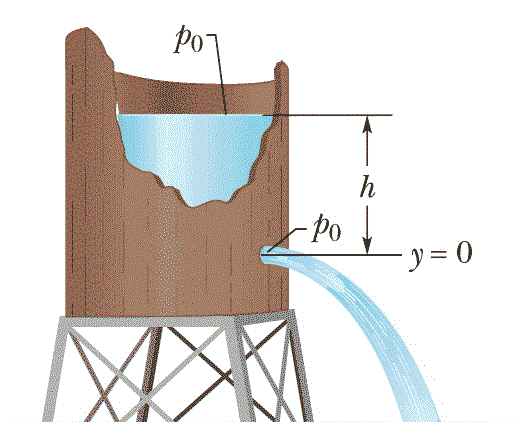
Evangelista Torricelli must have been watching some water jetting out of a water bottle one day when it dawned on him that the range and speed of the water reduced as its depth decreased. This is shown in the famous "spouting can" demonstration. The physics behind it is rather simple - the speed of the water exiting the hole depends on the pressure of the water and that in turn is directly related to the depth of the water. The gravitational potential energy of the hydrostatic pressure is converted to the kinetic energy of the water at the hole.
\[PE_{lost} = KE_{gained}\]
\[mgh=\frac{1}{2}mv^{2}\] Dividing everything by the volume, \(V\), gets rid of the awkward mass terms (as we don't know how much we are dealing with...) and replaces it with the density. \[\rho gh=\frac{1}{2}\rho v^{2}\] \[v = \sqrt{2gh}\] |
|
This result is identical to that met in Unit 1 - Kinematics for a falling object. As the water is being pulled down by the same force of gravity, this result should not be as surprising as it first seems. To follow through and calculate the range of the jet, we simply need to remember how to do projectiles. The lab work on this generally yields some pretty good data, unless it is windy....
11.5 - Bernoulli's Equation
Objectives:
- To understand how the conservation of energy leads to Bernoulli’s Equation
- To be able to use Bernoulli’s Equation to solve problems involving jets of water.
- To understand practical applications of the Bernoulli Effect.
|
Daniel Bernoulli was born in 1800 and came from a large family of scientists and mathematicians. In 1838 he applied the conservation of energy to a system of fluids flowing through a pipe that is at different heights. In doing so he created his famous equation. Torricelli's Theorem is simply a special case of the Bernoulli Equation.
|
|
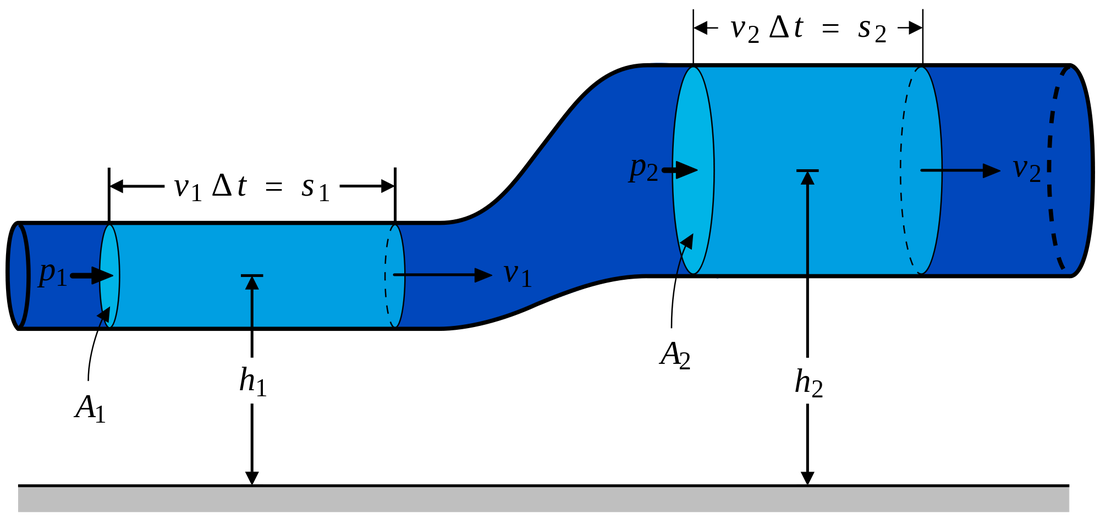
Consider a fluid flowing through a pipe that changes diameter as well as changing from a height \(h_1\) to a height \(h_2\). The fluid moves because it is under pressure. This pressure does work on the fluid. At the output end, the pressure of the moving fluid also does work (e.g. on a piston or something).
The work done on or by a fluid can easily be calculated by multiplying the pressure by the volume of the fluid. The power would then be the pressure multiplied by the flow rate. \[W = F\Delta x = \frac{F}{A}Ax = P\Delta V\] |
Note: This concept and relationship plays a critical role in thermodynamics as changing the volume and pressure of a gas involves work.
Applying the fundamental concept of the conservation of energy, the total energy going in must equal the total energy going out (ignoring any frictional losses). \[\left ( W+GPE+KE \right )_{1}=\left ( W+GPE+KE \right )_{2}\]
when substituting in the variables starts to become rather messy....
\[P_{1}V+mgh_{1}+\frac{1}{2}m v_{1}^{2}=P_{2}V+mgh_{2}+\frac{1}{2}m v_{2}^{2}\]
The volume of the liquid flowing must be conserved as the liquid is incompressible, so by dividing the whole equation by the volume \(V\) we get the longest equation in AP Physics:
\[P_{1}+\rho gh_{1}+\frac{1}{2}\rho v_{1}^{2}=P_{2}+\rho gh_{2}+\frac{1}{2}\rho v_{2}^{2}\]
Fortunately, usually many of the terms either cancel out or become zero.
when substituting in the variables starts to become rather messy....
\[P_{1}V+mgh_{1}+\frac{1}{2}m v_{1}^{2}=P_{2}V+mgh_{2}+\frac{1}{2}m v_{2}^{2}\]
The volume of the liquid flowing must be conserved as the liquid is incompressible, so by dividing the whole equation by the volume \(V\) we get the longest equation in AP Physics:
\[P_{1}+\rho gh_{1}+\frac{1}{2}\rho v_{1}^{2}=P_{2}+\rho gh_{2}+\frac{1}{2}\rho v_{2}^{2}\]
Fortunately, usually many of the terms either cancel out or become zero.
|
Water Fountains
During the summer of 2018, Kate and I visited the Alhambra in Granada, Spain. The summer gardens are very pretty, but the fascinating thing for a physicist is the engineering that went into the water system. In the Arab world running water is incredibly precious and to have freely running water through your palace is a sign of power. The water system is entirely gravity fed from a mountain stream high up in the Sierra Nevada mountains and led to the Alhambra, which is pretty high up on a rocky outcrop itself, via an 8 km aquaduct. This is still operational today, some 800 years after it was built. The pressure needed for these fountains comes from hydrostatic pressure due to the vertical height difference from the stream to the gardens. The water is not wasted, it continues to flow downwards through the gardens and into the fortress itself. |
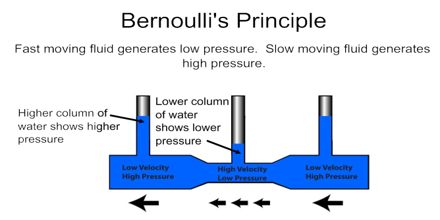
Bernoulli's Principle (Bernoulli Effect)
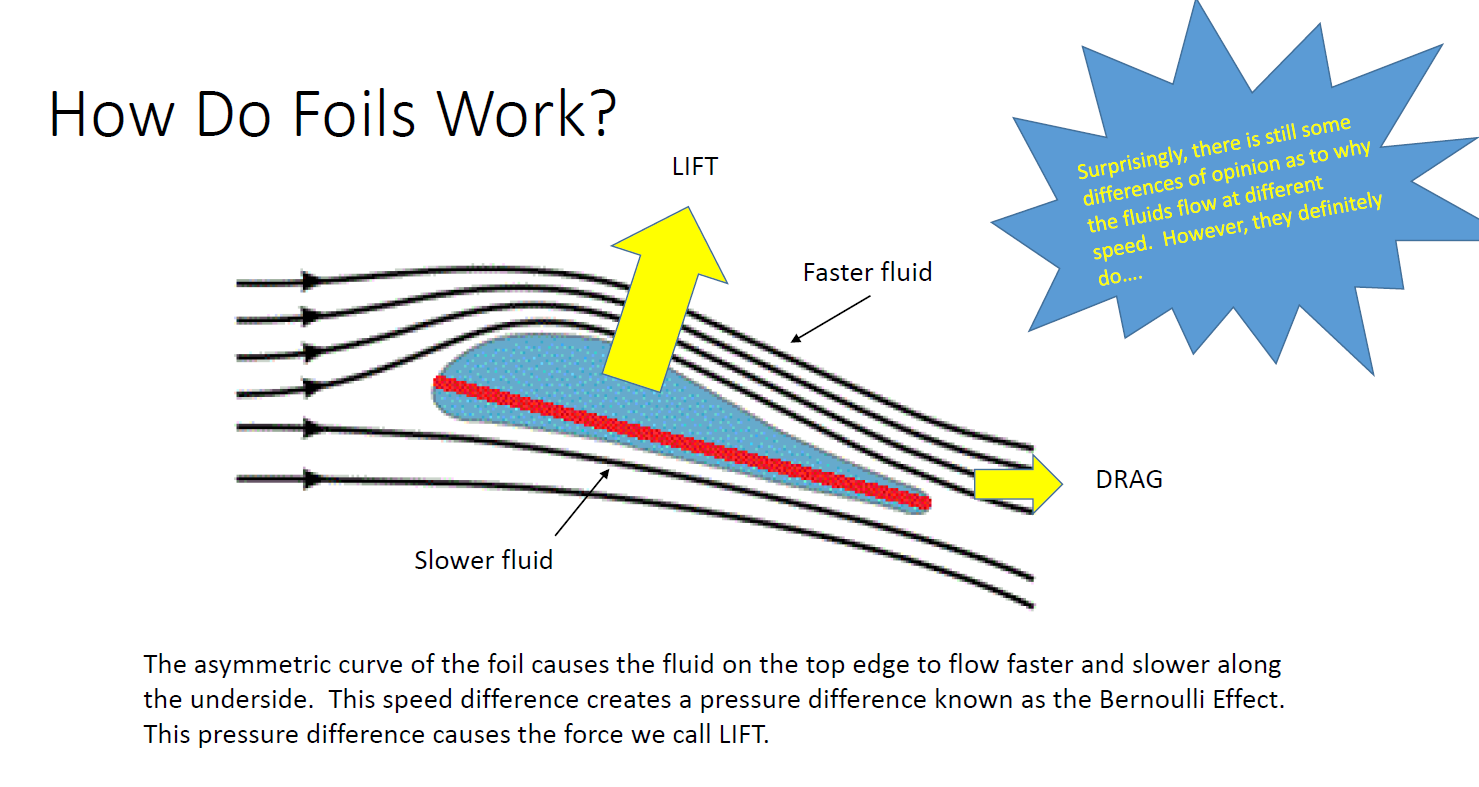
This staggeringly awesome effect is a consequence of the previous equation. For simplicity, assume that there is no change in vertical height, so the GPE terms cancel and vanish. We are then left with the Work (Pressure) and KE terms. A change in speed and hence KE implies that the Pressures must also change to compensate. Surprisingly, a faster moving fluid has a reduced pressure. This effect has had a huge impact on our lives. It is a strong contender for my favourite law of physics!
This staggeringly awesome effect is a consequence of the previous equation. For simplicity, assume that there is no change in vertical height, so the GPE terms cancel and vanish. We are then left with the Work (Pressure) and KE terms. A change in speed and hence KE implies that the Pressures must also change to compensate. Surprisingly, a faster moving fluid has a reduced pressure. This effect has had a huge impact on our lives. It is a strong contender for my favourite law of physics!
- differential airspeed over a curved wing creates a pressure difference, which in turn creates a force that lifts the wing up. We call this force LIFT, no matter which direction it acts in.
- the same effect provides the force that propels a sailing boat.
- the same effect provides the thrust from a propeller blade - or drives a wind turbine.
- the difference in speed of the water either side of a keel and rudder pulls a sailboat to windward.
- a Pitot tube uses this to measure the speed of an aircraft.
- The narrowing of the air intake of a carburettor increases the speed of the air and decreases its pressure, drawing in fuel from the reservoir.
- and many others....
|
|
Links
|
|
Computational Fluid Dynamics - #TechTuesday video produced by Oracle Team USA as part of the 2017 America's Cup Series.
|