Bermuda fitted dinghies racing in Granaway Deep. (Photo: Tom Clarke)
2.5 - Advanced Problems
Objectives:
- To be able to apply Newton’s Laws of Motion to solve complex problems – including forces at angles.
Blocks on slopes are really popular! Also the examiners love to come up with unusual situations.
Example 6
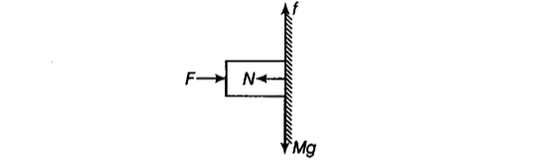
A student is holding a \(4 \,\text{kg}\) block against a wall with a coefficient of friction of \(0.5\). On inspection, the only upwards force is that of friction.
|
\[F_{up}=F_{down}\]
\[f=Mg\] |
\[F_{left}=F_{right}\]
\[F=N\] |
Combining the simultaneous equations with the friction equation will give:
\[f= \mu N =\mu F= Mg\]
\[F = \frac{Mg}{\mu }= \frac{40}{0.5}=80\,\text{N}\]
\[f= \mu N =\mu F= Mg\]
\[F = \frac{Mg}{\mu }= \frac{40}{0.5}=80\,\text{N}\]
Example 7
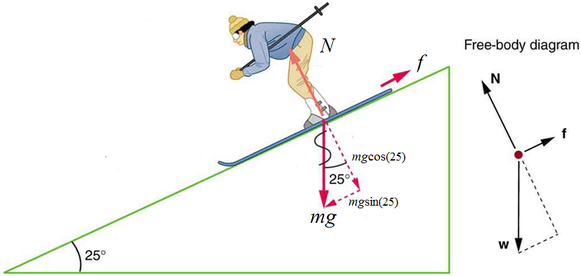
What is the acceleration of a \(60 \,\text{kg}\) skier as he glides down a slope at an angle of \(25^{\circ}\) with a coefficient of friction of \(0.1\)?
What is the acceleration of a \(60 \,\text{kg}\) skier as he glides down a slope at an angle of \(25^{\circ}\) with a coefficient of friction of \(0.1\)?
Taking 'UP' as out of the slope, the skier is not accelerating in that direction. So we can use statics. He is accelerating along the plane of the slope, so we must use \(F=ma\) for that direction:
|
Along the slope ('left/right')
\[F=ma\] \[mg\sin{(25)}-f=ma\] |
Out of slope ('up/down')
\[F_{up}=F_{down}\] \[N=mg\cos{(25)}\] |
Combining these with the friction equation gives:
\[f=mg\sin \left ( 25 \right )-ma=\mu mg\cos \left ( 25 \right )\]
\[a = g\sin \left ( 25 \right )-\mu g\cos \left ( 25 \right )\]
\[a = 3.3\text{m/s}^{2}\]
\[f=mg\sin \left ( 25 \right )-ma=\mu mg\cos \left ( 25 \right )\]
\[a = g\sin \left ( 25 \right )-\mu g\cos \left ( 25 \right )\]
\[a = 3.3\text{m/s}^{2}\]
Lab Work
There are plenty of standard lab assignments that are used in this topic. The classics are static set ups with newtonmeters or hanging masses to demonstrate Forces up = Forces down etc, measuring the acceleration of a trolley by a falling mass to demonstrate Newton's Second Law, connected blocks and measuring the coefficients of friction . However, at the end of the topic I like to set the students an involved project that draws together elements of this topic.
Some ideas include:
Some ideas include:
- Investigation into the factors that affect the final speed of a block of wood pulled up a slope by a falling mass.
- Investigation into how the angle of a slope affects the speed that a block of wood sliding downwards reaches the bottom.
- Measuring the parallel force needed to maintain a block's equilibrium varies with angle of a slope
- How the tension in a pair of identical strings supporting a mass vary as the included angle between them increases from 0 to 180 degrees.
- Using a bathroom scale to measure the acceleration of the school elevator. Compare with the accelerometer on a ipad.
- Use the principle of statics to measure the tension in a kite string.
Other Resources
Newton's Laws and Car Crashes - recommended by Morgan Kornarski of Safe Kids
|