Black Holes

Image from EHT via BBC News

It has been a very exciting time in astrophysics this week, with the first ever image of a black hole published across the news.  Here is a link to the BBC Science article.   So I thought that it would be a good exercise to do some AP-style physics on some of the data that has been published.  I have simplified things a bit as I don't know how to do calculations on rotating black holes and general relativity!

Size
The article states that the diameter of the event horizon is 40 billion km and its mass has been determined to be some 6.5 billion solar masses.  The mass could be calculated from the orbital speed (determined by the Doppler Effect) of the matter that forms the accretion disk surrounding the black hole, but no data on that is given in the article.  So, turning to classical physics, the event horizon is the radius where the escape velocity is equal to the speed of light.  The escape velocity is calculated from the law of conservation of energy.

\[KE_{lost}=PE_{gained}\]

\[\frac{1}{2}mv^{2}=\frac{GMm}{r}\]

A quick bit of algebra gives us:

\[r=\frac{2GM}{v^{2}}\]

\[r=\frac{2 \times 6.67\times 10^{-11}\times 6.5\times 10^{9} \times 2.0 \times 10^{30} }{(3\times10^{8})^{2}}\]

\[1.93\times 10^{13}\;\mathrm{m}\]

which gives a diameter of 38.5 billion km, which is very close to that quoted in the article!

The Rayleigh Criterion is the minimum separation that two point sources of light can have in order to be resolved as separate sources by an observer.  The blurring or spreading of the image is caused by the diffraction of light through the aperture of the observer's telescope lens.

Interferometry

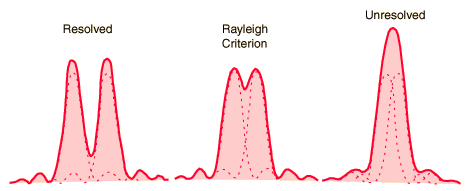
Essentially the limit of what we can see is determined by Rayleigh's Criterion (see AP-2 Unit 15), where the objects in question must diffract through the aperture of the telescope by less than their separation.  The variables that affect this are the diameter of the aperture through which diffraction occurs (the opening at the business end of a telescope), the subtended angle of the object, which depends on its size and distance from us, and finally, the wavelength of light observed.  The article does not specify the wavelength, but says that it is the high frequency end of radio.  Assuming that this value is 0.1 m, lets use the Rayleigh Criterion to determine the maximum size of the black hole that can resolved at the stated distance of 55 million light years using the EHT array shown above.

The Rayleigh Criterion for a circular aperture is:
​

\[\sin{\theta}=\frac{1.22 \lambda }{d}\]

As these are incredibly small angles the sine and tangent of the angle will be the same.

\[\frac{O}{A}=\frac{1.22 \lambda }{d}\]

where O = diameter of the black hole, A = distance from the Earth and d = diameter of the telescope.  Remembering that a light year is the distance traveled by light in one Earth year. 

\[\lambda=\frac{(40\times10^{9}\times10^{3}\times12000\times10^{3})}{(1.22 \times55\times10^{6}\times3\times10^{8}\times3.15\times10^{7})}\]

\[\lambda=7.57\times10^{-4}\;\mathrm{m}\]

which is in the microwave to infrared region of the EM spectrum.  Although I am sure that the effects of red shift due to both the expansion of the universe and the intense gravitational field of the black hole would have a significant effect on this calculation!

So, why would the black hole be a) so large and b) rotating?  The large part is easiest to understand, as the gravitational field is so strong matter would be drawn into the black hole, increasing its mass.  As its mass increases, the event horizon would expand further outwards and the gravitational field strength would further increase, creating a positive feedback cycle.  Eventually one could imagine that the black hole at the centre of that galaxy eventually consuming the entire galaxy.  Scary thought.  It may be possible to orbit a black hole, but the friction due to other incoming matter would probably cause the orbit to be unstable and quickly decay.  It is observed that stars rotate or spin.  It seems that the angular momentum of the star and its planets remains constant during stellar and planetary formation, therefore as the star's core collapses further to form a black hole, its angular velocity would increase.  Here, of course, we have another problem with classical physics.  As the black hole shrinks to a zero radius at its singularity (we think), then it angular velocity would tend towards infinity, which is certainly greater than the speed of light....  ah.....

Much has been reported about the fact that the team leader of this impressive international project is female.  What is astonishing is that this should be surprising!?  I know of at least two Bermudian females that have studied or are studying astrophysics at university.   Girls can be every bit as geeky as boys ya know.  

Katie Bouman, the MIT grad student that compiled all the synchronized data to form the image of the black hole. Photo from Katie Bouman via BBC News.