Hurricane Irma from space (September 2017)
|
Home >> AP Physics I >> Rotational Mechanics
|
next topic >>
|
This is a new topic for AP Physics 1. March 2014 was the first run through of it and we had to cobble up new experiments from whatever bits and bobs that we had laying around. We were grateful to CycleWorks for a donation of several old bike wheels! The AP examiners are feeling more confident about setting free response questions on this topic, consider yourself warned!
|
Bermuda Science Olympics 2014 - the task was to construct a machine that could raise a 1 kg mass off the floor to a height of 1 m, only using a rather feeble desk fan! We used the concept of varying torques due to the changing radius of a bike wheel (i.e. gearing and a rubber band drivetrain) to achieve the goal. Needless to say - we won!
Students then went on to use the apparatus to measure the torques, angular velocities and the different tangential velocities at the different radii. |
|
Hurricane Gonzalo - 17 October 2014. A hurricane is an extreme example of rotational mechanics. Last year the island suffered a direct hit. The eye lasted over an hour and the air was eerily still, with only the sound of tree frogs gleeping away. The worst part of the storm was the returning eye wall that brought the winds out of the west. The difference between the linear speed of the advancing storm and the tangential speed of the eye wall is enormous. The radar dome is situated to the east of the island near the airport and on the images is located at the cross-hairs in the centre.
Note: Hurricanes are not rigid bodies, but fluids, so they do not follow the equations and principles that we will be learning in this topic! |
7.1 - Getting to grips with rotational motion
|
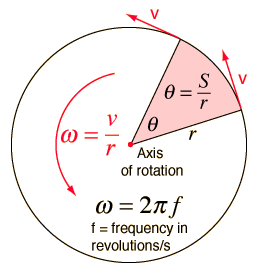
Rotational motion is slightly harder to conceptualise than linear motion. The key as far as I am concerned is to fully understand the variables that describe the rotation of an object. The easiest of these is the frequency, how many times the object rotates in 1 second. In reality, the timescale of seconds is often replaced by minutes. Therefore the frequency is quantified by the number of rotations per minute (rpm). This is often seen on bikes (e.g. a pedal bike may rotate at 70 rpm, and a motorbike engine at 2500 rpm). As with other applications, the period is the reciprocal of the frequency.
The tangential velocity is the same as with circular motion, and calculate by speed = distance/time = circumference/period. The tangential velocity decreases as the radius of the object decreases. In theory, the very centre of the axle is not moving! The final key variable for basic rotation is the angular velocity. This is the rate of change of angle. The simplest was to calculate this is 360 degrees/period. This will yield an angular velocity in degrees per second. In the more useful units of radians:
The tangential velocity is the same as with circular motion, and calculate by speed = distance/time = circumference/period. The tangential velocity decreases as the radius of the object decreases. In theory, the very centre of the axle is not moving! The final key variable for basic rotation is the angular velocity. This is the rate of change of angle. The simplest was to calculate this is 360 degrees/period. This will yield an angular velocity in degrees per second. In the more useful units of radians:
|
Clocks
The clock on the left is on Reid Street, Hamilton. On the right is Big Ben on the Houses of Parliament, London. The angular velocities of the minute and hour hands of every clock in the world are the same. i.e. The minute hand sweeps through 360 degrees in one hour everywhere. However, the tip of the minute hand of Big Ben moves faster than that of the Reid Street clock as its radius length is far greater. |
If you are comfortable with these variables and with chopping and changing between them, that is half the battle with this unit.
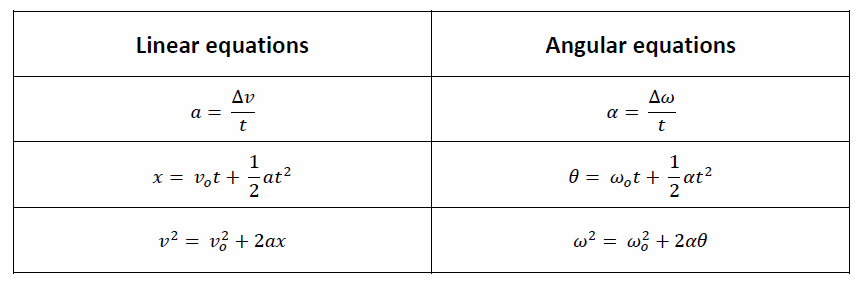
The equations below are the LINKING equations between linear and rotational variables. You just need to learn one of these and the others follow the same pattern. As an aide memoire I use the middle one and check whether the velocity tends to zero as the radius tends to zero to check I have the right way around...
They follow the pattern: LINEAR VARIABLE = RADIUS x ROTATIONAL VARIABLE
\[s=r\theta\]
\[v=r\omega\]
\[a=r\alpha\]
The equations below are the LINKING equations between linear and rotational variables. You just need to learn one of these and the others follow the same pattern. As an aide memoire I use the middle one and check whether the velocity tends to zero as the radius tends to zero to check I have the right way around...
They follow the pattern: LINEAR VARIABLE = RADIUS x ROTATIONAL VARIABLE
\[s=r\theta\]
\[v=r\omega\]
\[a=r\alpha\]
The kinematics equations are practically the same as the three that you learned from Unit 1 - Kinematics. We have simply replaced the linear variable with its rotational equivalent. (angle for displacement, angular velocity for velocity and angular acceleration for acceleration). They can be converted back and forth using the linking equations above. You will be measuring these in the lab and performing numerous calculations.
Gibb's Hill Lighthouse
The lighthouse appears to have a flashing light on the top. In reality it is a fixed light and a revolving set of five lenses. The lenses sit on a mercury bearing, which famously become inoperative after Hurricane Fabian in 2003. Originally the rotation was powered by a system of gears that were powered by a torque provided by a 1200 lb mass that ran through the centre of the lighthouse. This had to be re-hoisted to the top of the lighthouse every 5 hours! These days, an electric motor under a plywood box causes the rotation of the beams.
Data: On a humid night it is possible to see the 5 beams of light rotating out from the lantern. The period of rotation was measured as 45 seconds. What is the angular velocity and what is the flash rate of the lighthouse as seen from a ship? What would be the tangential speed of the beams some 26 km out to sea? From the video, can you estimate the angular velocity of the radar?
The lighthouse appears to have a flashing light on the top. In reality it is a fixed light and a revolving set of five lenses. The lenses sit on a mercury bearing, which famously become inoperative after Hurricane Fabian in 2003. Originally the rotation was powered by a system of gears that were powered by a torque provided by a 1200 lb mass that ran through the centre of the lighthouse. This had to be re-hoisted to the top of the lighthouse every 5 hours! These days, an electric motor under a plywood box causes the rotation of the beams.
Data: On a humid night it is possible to see the 5 beams of light rotating out from the lantern. The period of rotation was measured as 45 seconds. What is the angular velocity and what is the flash rate of the lighthouse as seen from a ship? What would be the tangential speed of the beams some 26 km out to sea? From the video, can you estimate the angular velocity of the radar?
|
A cloudy winter's day in Bermuda! Left, Gibb's Hill lighthouse and above, the original mechanism that converted the linear motion of the descending mass to the rotational motion of the lenses. In the foreground, the shaft and dog clutch for the modern electric motor can be seen. The bevelled gear serves no purpose now. There would have been a winding handle for the keeper to winch up the driving mass.
|
|
|
Video of the radar at the top of the lighthouse. This and another one at Fort George can fix the position of every ship around the island.
|
\[v=r\omega\] As the radius increases, the tangential (linear) velocity increases.
7.2 - Rotational Dynamics
|
Rotational Inertia
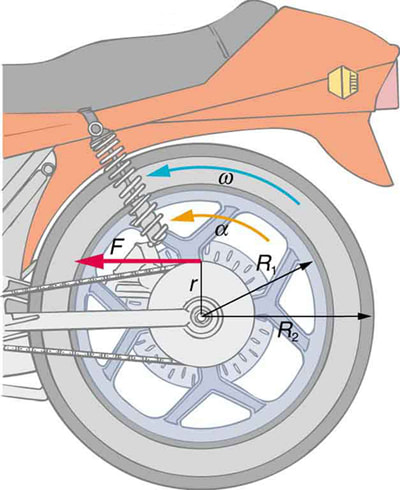
Now for the hardest concept: In order to change the rotation of an object you require a torque - this is simply the tangential force applied x the radial distance of the force. But the object will resist the change in motion, much the same way that any object resists a change in linear motion. In the linear case this resistance to motion is due to the mass or inertia of the object. For rotating bodies, this inertial property is called the rotational inertia (or moment of inertia). The larger the rotational inertia the harder it is to change the speed rotation. Mathematically the rotational inertia is defined as the required torque/(change in angular velocity), much the same way as mass = required force/acceleration for linear motion. Newton's first and second law still apply. In the absence of a resistive torque a spinning object will continue to spin forever. The Earth being an excellent example!
The rotational inertia of object is a function of their geometry. Mathematically it is always a function of *mr2 (coefficient x mass x radius squared). The coefficient can be determined by considering where the centre of mass of a radial section is. If the centre of mass is at the rim them I = mr2. If it is half way to the rim then I = 1/2mr2. Objects with the mass towards the rim are harder to change the rotation of than objects with the mass concentrated towards the centre.
\[I = (coeff)mr^{2}\]
Now for the hardest concept: In order to change the rotation of an object you require a torque - this is simply the tangential force applied x the radial distance of the force. But the object will resist the change in motion, much the same way that any object resists a change in linear motion. In the linear case this resistance to motion is due to the mass or inertia of the object. For rotating bodies, this inertial property is called the rotational inertia (or moment of inertia). The larger the rotational inertia the harder it is to change the speed rotation. Mathematically the rotational inertia is defined as the required torque/(change in angular velocity), much the same way as mass = required force/acceleration for linear motion. Newton's first and second law still apply. In the absence of a resistive torque a spinning object will continue to spin forever. The Earth being an excellent example!
The rotational inertia of object is a function of their geometry. Mathematically it is always a function of *mr2 (coefficient x mass x radius squared). The coefficient can be determined by considering where the centre of mass of a radial section is. If the centre of mass is at the rim them I = mr2. If it is half way to the rim then I = 1/2mr2. Objects with the mass towards the rim are harder to change the rotation of than objects with the mass concentrated towards the centre.
\[I = (coeff)mr^{2}\]
|
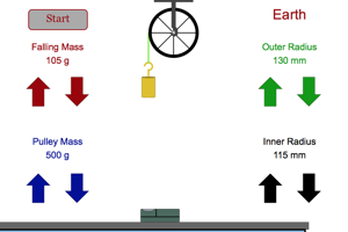
Physics Aviary - Virtual Lab
This is a simulation of the real lab that we do in class, although we can't change the goemetry of the wheel as this one can do. Variables include the mass of the pulley and the suspended object as well as the inner and outer radius of the pulley. The most interesting is changing from a hoop to a disk, but keeping the masses the same. The moment of interia of a disk is half of that of a hoop of the same radius and mass. (Another great HTML V simulation from Frank McCulley.) |
|
|
LAB WORK: Jordan uses a descending mass to rotate a T-bar with some hanging masses.
|
7.3 - Angular Momentum
|
|
|
Jake Fisher demonstrating the conservation of Angular Momentum - 16 April 2014 (video by Kurt Repose)
|
7.4 - Rotational Kinetic Energy
|
Rotational Kinetic Energy
Rotating bodies are moving and therefore will require work to be done to stop them. So they have kinetic energy. The equation for this rotational energy is similar to the linear version:
\[KE_{linear} = \frac{1}{2}mv^{2}\]
\[KE_{rotational} = \frac{1}{2}I\omega ^{2}\]
When an object is rolling along the ground, it has two forms of kinetic energy- the linear KE of normal motion and the kinetic energy of the rotation. This becomes really important when we have objects rolling down hills!
Applying the conservation of energy:
\[PE = KE_{linear}+KE_{rotational}\]
When an object rolls down a slope some of the gravitational potential energy is transferred into rotational energy instead of just purely into linear kinetic energy. The object moves slower. The higher the rotational inertia of the object, the slower it moves down the hill.
Rotating bodies are moving and therefore will require work to be done to stop them. So they have kinetic energy. The equation for this rotational energy is similar to the linear version:
\[KE_{linear} = \frac{1}{2}mv^{2}\]
\[KE_{rotational} = \frac{1}{2}I\omega ^{2}\]
When an object is rolling along the ground, it has two forms of kinetic energy- the linear KE of normal motion and the kinetic energy of the rotation. This becomes really important when we have objects rolling down hills!
Applying the conservation of energy:
\[PE = KE_{linear}+KE_{rotational}\]
When an object rolls down a slope some of the gravitational potential energy is transferred into rotational energy instead of just purely into linear kinetic energy. The object moves slower. The higher the rotational inertia of the object, the slower it moves down the hill.
|
|
|
Hurricanes Maria and Irma 2017 - This video shows how a hurricane has both linear motion (KE-linear) and rotational motion (KE-rotational). This is just as they both swept through the Caribbean as category 5 storms.
Revision Sheets
Other Resources
|
YouTube clip - rigid body rotation lecture
|