2 - Dynamics
More sophisicated animations can be made that are based on the forces applied to the object. There are two ways to do this, which are essentially the same. In both cases I will use \(r\) to represent the position vector of the object. In the code \(\Delta t\) becomes \(dt\) as coding cannot use Greek letters.
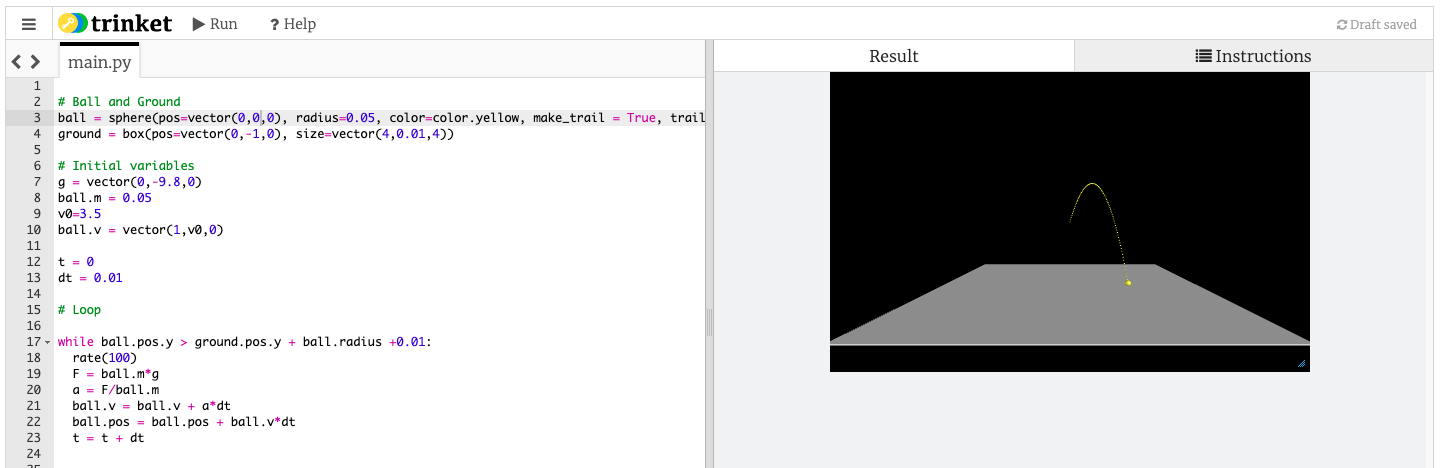
Method 1
This uses the force to calculate the acceleration using Newton's Second Law and then kinematics:
\[a = \frac{F}{m}\]
\[v = v_0 + a\Delta t\]
\[r = r_0+v \Delta t\]
Method 2
This is based on momentum:
\[ p = p_0 +F \Delta t\]
\[r = r_0 +\frac{p \Delta t}{m}\]
Method 1
This uses the force to calculate the acceleration using Newton's Second Law and then kinematics:
\[a = \frac{F}{m}\]
\[v = v_0 + a\Delta t\]
\[r = r_0+v \Delta t\]
Method 2
This is based on momentum:
\[ p = p_0 +F \Delta t\]
\[r = r_0 +\frac{p \Delta t}{m}\]
Force Vectors
Forces are vectors with both a magnitude and direction. Sometimes the direction is fixed, for example small scale gravity acts downwards or the force due to a uniform electric field. On many occasions, the direction of the force changes. This is where UNIT VECTORS come in. For example, if the force relates to the position vector \(r\), then the unit vector has the same direction but a magnitude of 1. This is denoted as \(\hat{r}\).
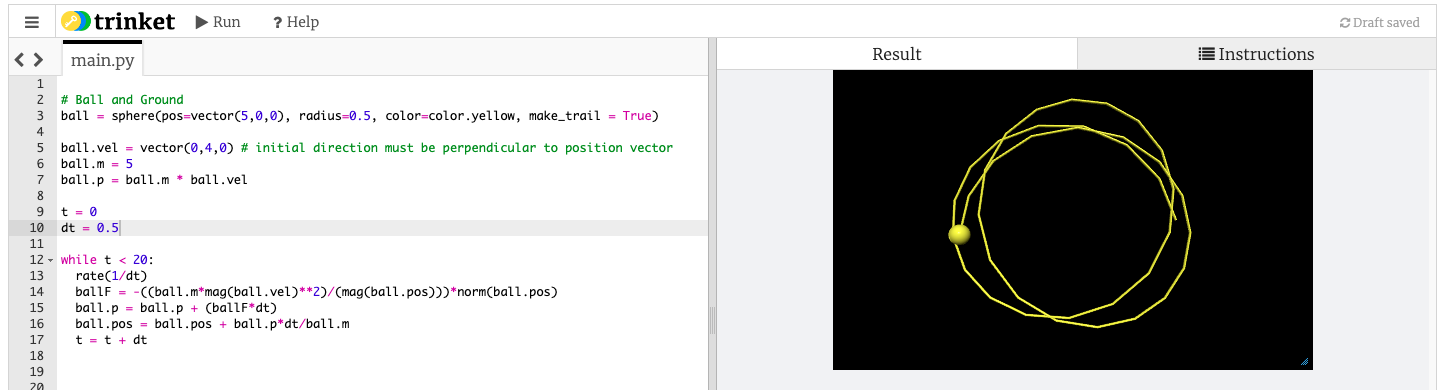
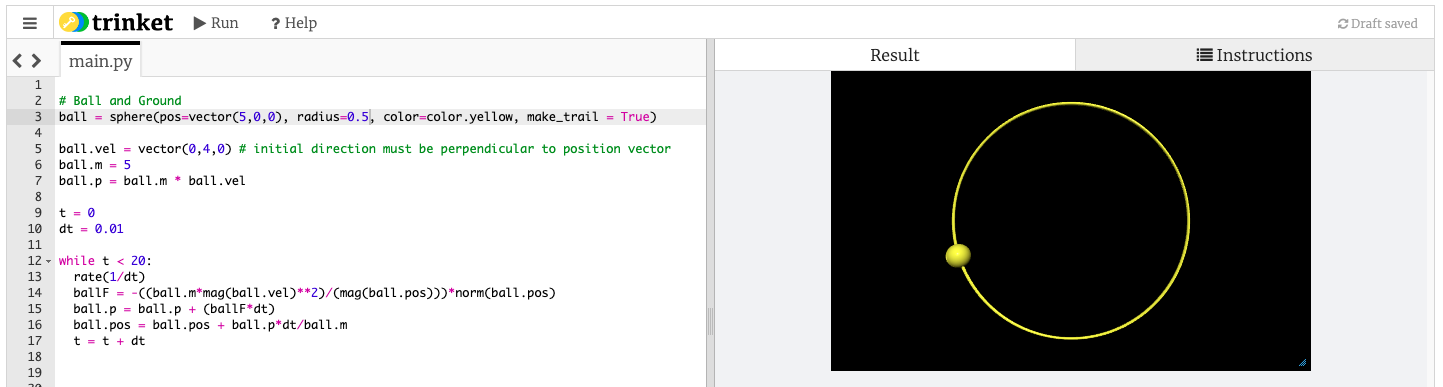
Example: Centripetal force. The centripetal force on an object moving at speed v around a circle of radius R is:
\[F_c= \frac{mv^2}{R}\]
But when we square a vector, it blows up. So we need to square the magnitude of the vectors, which would result in a scalar quantity. To solve this, we then multiply the answer by the unit vector. As the force is attractive and the acting in the opposite direction to the position vector, we would need a minus sign:
\[F = -\frac{m |v|^2 }{|R|} \hat{r}\]
We could calculate the magnitude of the vectors inside the loop using Pythagoras, but luckily there exists a function that will do that easily - mag(vel). The unit vector direction could be calculated using trigonometry, but there is also a simpler function - norm(pos).
Forces are vectors with both a magnitude and direction. Sometimes the direction is fixed, for example small scale gravity acts downwards or the force due to a uniform electric field. On many occasions, the direction of the force changes. This is where UNIT VECTORS come in. For example, if the force relates to the position vector \(r\), then the unit vector has the same direction but a magnitude of 1. This is denoted as \(\hat{r}\).
Example: Centripetal force. The centripetal force on an object moving at speed v around a circle of radius R is:
\[F_c= \frac{mv^2}{R}\]
But when we square a vector, it blows up. So we need to square the magnitude of the vectors, which would result in a scalar quantity. To solve this, we then multiply the answer by the unit vector. As the force is attractive and the acting in the opposite direction to the position vector, we would need a minus sign:
\[F = -\frac{m |v|^2 }{|R|} \hat{r}\]
We could calculate the magnitude of the vectors inside the loop using Pythagoras, but luckily there exists a function that will do that easily - mag(vel). The unit vector direction could be calculated using trigonometry, but there is also a simpler function - norm(pos).
The code above models circular motion using method 2. The direction of the force is determined by the norm(ball.pos) vector. The time step was made delibrately large to highlight the fundamental problems of computer simulations. They can't do calculus (the maths of continuous change), but rather calculations over a finite time step. If the time step is made small enough, the straight lines become so short as to become insigificant. This is very important to understand. The smaller the time step, the ore accurate the model, but the more calculations per second are required to run it, so a more powerful computer is required. When models get very complex, this means that massive supercomputers are needed to simulate reality. Think about how video games have gotten more realistic as computers have become ever more powerful.
ACTIVITIES
- Vary the radius and speed of the object moving in a circle.
- Place a red ball in the centre of the circle, so that it looks like an orbit.
- Change the orientation of the circle - the code can do 3-D.
- Have two balls of different colours moving in different circles, or the same circle.