|
Waves >>
|
Photo: Warwick Long Bay, Bermuda. There are all three states of matter in this photo: Solid - sand and rocks, Liquid - the ocean and the clouds, Gas - the atmosphere.
This topic covers the concepts of density and pressure, and then applies them to the states of matter, especially liquids and gases. The behaviour of gases to changes of pressure, volume and temperature are studied, as is the concept of absolute zero.
This topic covers the concepts of density and pressure, and then applies them to the states of matter, especially liquids and gases. The behaviour of gases to changes of pressure, volume and temperature are studied, as is the concept of absolute zero.
3.1 - Density
- Recall and use the relationship between density, mass and volume.
- Describe how to determine density using direct measurements of mass and volume.
|
|
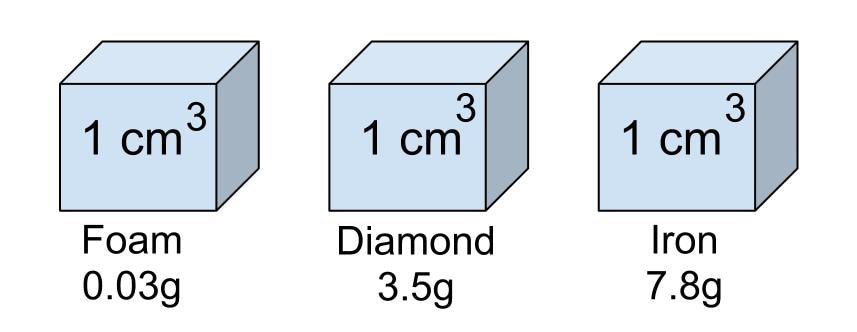
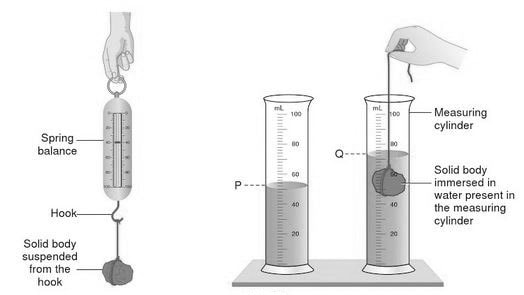
Density is a measure of how heavy something is for its size. The heavy bit is measured as MASS, the size bit as VOLUME. Measuring the mass is usually straightforward - put on a balance. Measuring the volume rather depends on the shape. If it is a regular shape, it is easiest and most accurate to use maths. E.g for a cuboid the volume is simply the product of the length, width and height. If the shape is irregular then the easiest method is to use the displacement of water method famously discovered by Archimedes of Syracuse. Small objects can be placed directly in a measuring cylinder or equivalent. Larger objects we use a Eureka can and measure the volume of the overflow. It is an interesting exercise to compare the theoretical volumes of regular objects with that measured by displacement.
The density is calculated using the equation below:
The density is calculated using the equation below:
\[\rho =\frac{m}{V}\]
Units are either \(\text{kg/m}^3\) or \(\text{g/cm}^3\). Note that these are not equivalent! The density of a material is constant and is a measure of a) how heavy the molecules are and b) how closely packed they are to each other. The density of water is 1 g/cm3 or 1000 kg/m3. This means that a cubic metre of water weighs a tonne! We really appreciate this when bailing water out of a swamped boat.
Cubes of water along Front Street left over from the World Triathlon event. The sides are 1.0 m, so the mass of the water would be exactly 1000 kg (1 metric tonne).
|
May 24th Race 2014. Victory sinking in a big way during a tack. Your physics teacher's head can just be seen! Recovering the boat by hand after a sink is very difficult as the whole boat is full of water - at least a tonne of it!
|
If the density of any substance is greater than that of water it sinks, less it floats. Oil is less dense than water so rises to the top. Surprisingly, ice is less dense than water, so it floats!
|
PhET Simulation - Buoyancy. Here you can play by changing the density or volume of cubes and seeing whether they float or sink. Advanced students can investigate the buoyancy force (upthrust) and see how it depends on the volume submerged and the density of the fluid.
|
3.2 - Pressure
- Recall and use the relationship between pressure, force and area.
- Understand that the pressure at a point in a gas or liquid which is at rest acts equally in all directions.
- Recall and use the relationship for pressure difference.
When a force is exerted on something, it is generally applied over an area. The force could be spread out over a large area or concentrated onto a small area. This concentration of a force is known as pressure. The equation is:
\[P = \frac{F}{A}\]
The units of pressure are usually N/m2 (called Pascals), or N/cm2. The imperial units of psi (lb/in2) are still commonplace on the island and in the US. Meteorology uses millibars.
\[P = \rho gh\]
3.3 - States of Matter
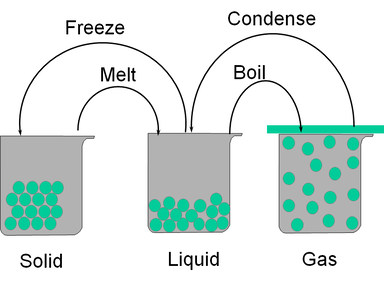
- Understand that a substance can change state from solid to liquid by the process of melting.
- Understand that a substance can change state from liquid to gas by the process of evaporation or boiling.
- Recall that particles in a liquid have a random motion within a close-packed structure.
- Recall that particles in a solid vibrate about fixed positions within a close-packed regular structure.
|
|
3.4 - Kinetic Theory
- Understand the significance of Brownian motion.
- Recall that molecules in a gas have a random motion and that they exert a force and hence a pressure on the walls of the container.
- Understand that there is an absolute zero of temperature which is – 273 °C.
- Describe the kelvin scale of temperature and be able to convert between the Kelvin and Celsius scales.
Kinetic Theory is the idea that all matter is made up from moving particles. The hotter the material, the faster the particles (atoms/molecules) are moving. In a solid, the motion is vibration about a fixed location in the lattice. With liquids and gases the motion is much more free. This leads to the concept of what is temperature. On a fundamental level the absolute temperture is proportional to the mean kinetic energy of the particles:
\[T\propto \bar{KE}\]
This is different from the concept of heat. The heat contained within a substance is the total kinetic energy of all of the particles combined.
It follows then that if a substance was cooled to the extent that all particle motion/vibration ceased the temperature would be zero. This is predicted to occur at \(-273^{\circ} \text{C}\), which is given a special name - absolute zero.
To make the maths work we use a temperature scale that is zeroed on absolute zero. This is the Kelvin scale. To convert from degrees Celsius to Kelvin is easy, just add 273. Note that we omit the degrees when quoting Kelvin temperatures.
e.g.
\[100^{\circ} \text{C} + 273 = 373 \text{ K}\]
\[T\propto \bar{KE}\]
This is different from the concept of heat. The heat contained within a substance is the total kinetic energy of all of the particles combined.
It follows then that if a substance was cooled to the extent that all particle motion/vibration ceased the temperature would be zero. This is predicted to occur at \(-273^{\circ} \text{C}\), which is given a special name - absolute zero.
To make the maths work we use a temperature scale that is zeroed on absolute zero. This is the Kelvin scale. To convert from degrees Celsius to Kelvin is easy, just add 273. Note that we omit the degrees when quoting Kelvin temperatures.
e.g.
\[100^{\circ} \text{C} + 273 = 373 \text{ K}\]
3.5 - Specific Heat Capacity
- Know that specific heat capacity is the energy required to change the temperature of 1 kg of mass by 1 °C.
- Be able to use the equation for the heating of a substance.
|
When we heat a substance, we are adding thermal energy to it and the temperature rises. On a molecular level, we are increasing the KE of the particles and they move around faster. Remember that the absolute temperature is proportional to the mean KE. However, the amount the temperature increases by is a function of a number of variables:
\[E=mc\Delta T\] |
|
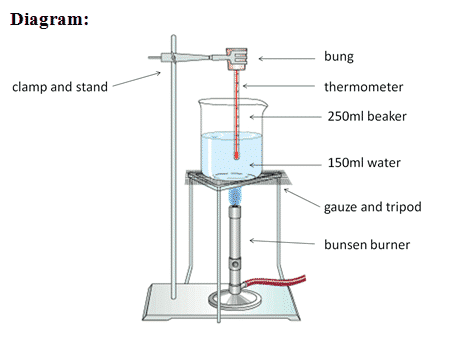
We will be performing a lab experiment to try to measure the specific heat capacity of a variety of materials. We will be heating the materials up wth an electric immersion heater for 10 mins (600 s) and measuring the temperature rise. The energy input is determined by multiplying the current and the voltage that is displayed on the power supply and the time in seconds. The specific heat capacity is then found by:
\[c=\frac{E}{m\Delta T}\] Provided that the heater has been pre-heated and the the material has been well insulated, the typical experimental values should be close to the official ones:
|
Material |
Specific Heat Capacity (J/kgK) |
water |
4200 |
sand |
800 |
copper |
390 |
aluminium |
900 |
iron |
450 |
3.6 - The Gas Laws - The Pressure Law
- understand that an increase in temperature results in an increase in the speed of gas molecules.
- understand that the Kelvin temperature of the gas is proportional to the average kinetic energy of its molecules.
- describe the qualitative relationship between pressure and kelvin temperature for a gas in a sealed container.
- use the relationship between the pressure and Kelvin temperature of a fixed mass of gas at constant volume.
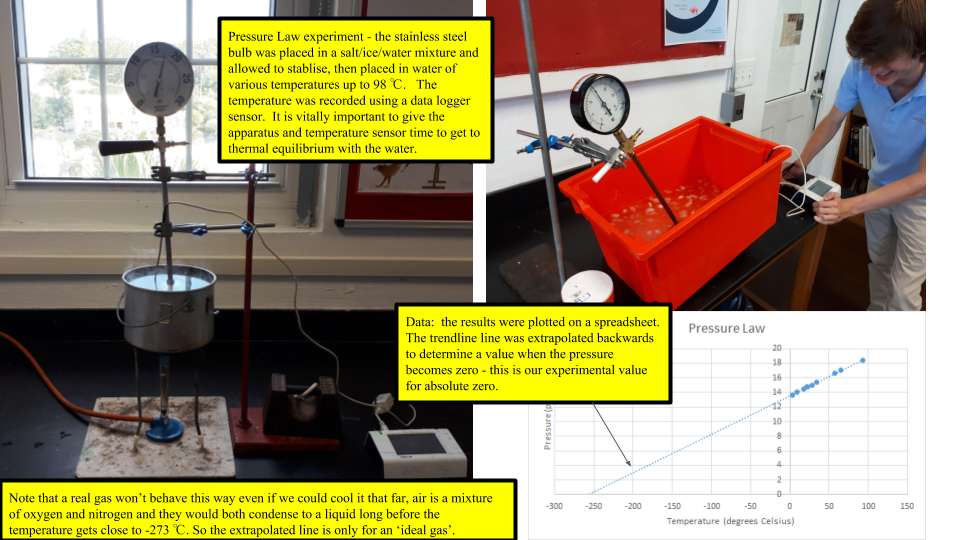
If you take a sealed empty soda bottle and place in it ice water, it collapses. Move the same bottle to a bucket of hot water, it reinflates and becomes firm again. Switching between the two temperatures has a predictable and consistent effect. The mass of the air inside the bottle is fixed, but as it is heated the particles inside gain energy and move faster. Therefore, the strike the walls of the bottle faster and more frequently. This exerts more force over the area of the walls and increases the pressure. Using a more sophisticated apparatus of a stainless steel ball and a pressure gauge we can quantify this effect - known as the Pressure Law. Plotting a graph of the data yields a nice straight line - but not one that is zeroed on the origin. Extrapolating (always slightly dodgy) the line back to the point where the pressure is zero - which means that all atomic motion has stopped and the particles are no longer hitting the walls of the container - yields a resulting temperature of -273 deg Celsius. This is known as ABSOLUTE ZERO.
Re-zeroing the temperature scale to start at absolute zero shows us that the pressure is directly proportional to the temperature in Kelvins - and so the following equation works nicely:
\[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\]
Re-zeroing the temperature scale to start at absolute zero shows us that the pressure is directly proportional to the temperature in Kelvins - and so the following equation works nicely:
\[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\]
It is IMPORTANT to remember that the Celsius temperatures will not work. For example, a fixed mass of gas at \(100^{\circ}\mathrm{C}\) and at atmospheric pressure is cooled to \(-10^{\circ}\mathrm{C}\) . What is the final pressure?
|
In Celsius
\[\frac{P_{1}}{T_{1}}=\frac{P_{2}}{T_{2}}\] Using the Celsius values in the equation: \[\frac{1}{100}=\frac{P_{2}}{-10}\] \[P_{2}=-0.1\,\mathrm{atm}\] which is clearly impossible as we can't have negative pressure! |
In Kelvin
\[ 100^{\circ} \mathrm{C}=373\,\mathrm{K} \] \[ -10^{\circ} \mathrm{C}=263\,\mathrm{K} \] so, substituting the Kelvin values into the equation leads to: \[\frac{1}{373}=\frac{P_{2}}{263}\] \[P_{2}=0.71\,\mathrm{atm}\] |
3.7 - The Gas Laws - Boyle's Law
- use the relationship between pressure and volume of a fixed mass of gas at constant temperature.
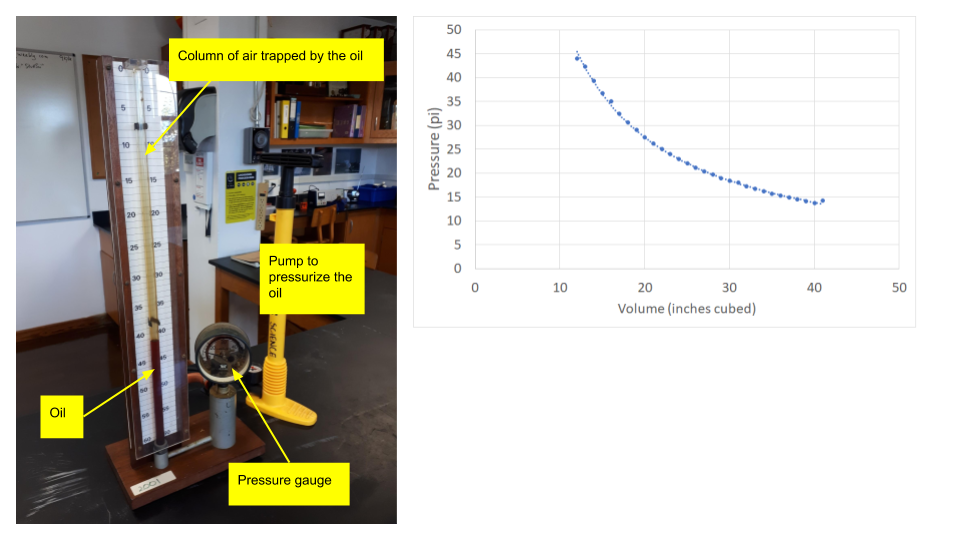
If we increase the external pressure on a gas it gets smaller as the particles are pushed closer together. This is easily experienced by squeezing an empty water bottle. We can do this is in the lab with a syringe and a pressure sensor, or using the large apparatus shown below. As the pressure increases, the volume of the gas gets ever smaller. The converse is also true - as we release the pressure, the gas expands. The pressure and volume are inversely proportional. If we consider two states, before a change (1) and after the change (2), we get the equation for Boyle's Law:
\[P_{1}V_{1}=P_{2}V_{2}\]
The units of pressure and volume do not matter, but need to be consistent.
example:
A dive tank contains 8 litres of air at 200 atm (200 x atmospheric pressure). What volume of air will be released at normal atmospheric pressure?
Step 1 - identify the variables:
\[P_1 = 200 \text{ atm,} \text{ } V_1 = 8 \text{ L,} \text{ } P_2 = 1 \text{ atm,} \text{ } V_2 = \text{ ? }\]
Step 2 - apply the equation:
\[P_{1}V_{1}=P_{2}V_{2}\]
rearrange:
\[V_2 = \frac{P_1 V_1}{P_2}\]
\[V_2 = \frac{200 \times 8}{1} = 1600\text{ L}\]
We can go further, for example if a diver requires 16 litres of air a minute, how long will his air tank last?
\[t = \frac{1600 \text{ L}}{16} = 100 \text{ minutes}\]
\[P_{1}V_{1}=P_{2}V_{2}\]
The units of pressure and volume do not matter, but need to be consistent.
example:
A dive tank contains 8 litres of air at 200 atm (200 x atmospheric pressure). What volume of air will be released at normal atmospheric pressure?
Step 1 - identify the variables:
\[P_1 = 200 \text{ atm,} \text{ } V_1 = 8 \text{ L,} \text{ } P_2 = 1 \text{ atm,} \text{ } V_2 = \text{ ? }\]
Step 2 - apply the equation:
\[P_{1}V_{1}=P_{2}V_{2}\]
rearrange:
\[V_2 = \frac{P_1 V_1}{P_2}\]
\[V_2 = \frac{200 \times 8}{1} = 1600\text{ L}\]
We can go further, for example if a diver requires 16 litres of air a minute, how long will his air tank last?
\[t = \frac{1600 \text{ L}}{16} = 100 \text{ minutes}\]
Note: Boyle's Law is only strictly true if the pressure acting on a gas is changed slowly. If a gas is rapidly compressed it will heat up. Squeezing it slowly allows this heat to leave and time for the temperature to again match its surroundings. The opposite is also true, rapid expansion of a gas reduces its temperature. Neither of these situations will be included on the IGCSE exam.
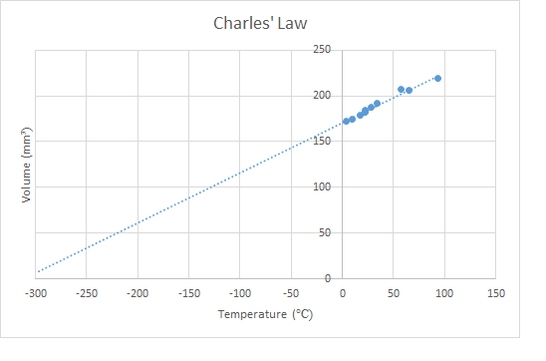
3.8 - The Gas Laws - Charles' Law (not examined)
- Describe the qualitative relationship between volume and kelvin temperature for a gas in a container that is free to expand or contract.
- Use the relationship between the Volume and Kelvin temperature of a fixed mass of gas at constant pressure.
The third of the gas laws concerns the heating of a gas while maintaining constant pressure. The increased speed of the particles causes them to spread out more and expanding the gas. This is called thermal expansion and ultimately is the cause of convection in gases. The relationship is similar to the pressure law, the volume is proportional to the absolute temperature. In the lab this can be demonstrated by putting a sealed gas syringe into water baths of different temperatures or by using the apparatus shown below. Sadly, neither of these experiments tend to give particularly accurate results, but do show the basic idea.
Charles' Law is defined mathematically by the equation below. As with the pressure law, it is critical to convert the temperature units from Celsius to Kelvin.
\[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\]
Charles' Law is defined mathematically by the equation below. As with the pressure law, it is critical to convert the temperature units from Celsius to Kelvin.
\[\frac{V_{1}}{T_{1}}=\frac{V_{2}}{T_{2}}\]
|
The apparatus on the left is a narrow glass tube with one end sealed and the other end with some oil in it. The oil traps some air. As the trapped air is heated, the oil moves upwards so that the pressure is always equal to atmospheric pressure. The key is to heat it slowly so that the temperature of the trapped air is equal to that of the water surrounding it.
|
3.9 - The Gas Laws - The Universal Gas Law (not examined)
- Be able to use the combined gas law relationship between the volume, pressure and Kelvin temperature of a fixed mass of gas.
The three gas laws can be combined into one universal gas law, which is a lot easier to remember and required when all three variables are changing:
\[\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\]
example:
A weather balloon of volume \(0.8 \text{ m}^3\) is launched from Bermuda weather station. At ground level the pressure is \(1 \text{ atm}\) and the temperature is \(25^{\circ} \text{C}\). In the stratosphere the pressure and the temperature drop to \(0.01\text{ atm}\) and \( - 50^{\circ} \text{C}\). What is the new volume of the balloon?
Step 1 - identify the variables:
\[P_1 = 1 \text{ atm,} \text{ } V_1 = 0.8 \text{ m,}^3 \text{ } T_1 = 25 + 273 = 298 \text{ K,} \text { }P_2 = 0.01 \text{ atm, } T_2 = -50+273 = 223 \text{ K, } V_2 = \text{ ? }\]
Step 2 - apply the equation:
\[\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\]
rearrange:
\[V_2=\frac{P_{1} V_{1} T_{2}}{P_2 T_{1}}\]
\[V_2=\frac{1 \times 0.8 \times 223}{0.01 \times 298}\]
\[V_2 = 59.87\text{ m}^3\]
\[\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\]
example:
A weather balloon of volume \(0.8 \text{ m}^3\) is launched from Bermuda weather station. At ground level the pressure is \(1 \text{ atm}\) and the temperature is \(25^{\circ} \text{C}\). In the stratosphere the pressure and the temperature drop to \(0.01\text{ atm}\) and \( - 50^{\circ} \text{C}\). What is the new volume of the balloon?
Step 1 - identify the variables:
\[P_1 = 1 \text{ atm,} \text{ } V_1 = 0.8 \text{ m,}^3 \text{ } T_1 = 25 + 273 = 298 \text{ K,} \text { }P_2 = 0.01 \text{ atm, } T_2 = -50+273 = 223 \text{ K, } V_2 = \text{ ? }\]
Step 2 - apply the equation:
\[\frac{P_{1}V_{1}}{T_{1}}=\frac{P_{2}V_{2}}{T_{2}}\]
rearrange:
\[V_2=\frac{P_{1} V_{1} T_{2}}{P_2 T_{1}}\]
\[V_2=\frac{1 \times 0.8 \times 223}{0.01 \times 298}\]
\[V_2 = 59.87\text{ m}^3\]
|
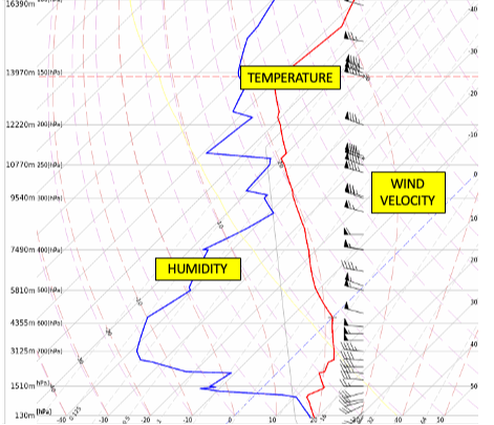
A weather balloon being launched from BWS. These are released twice a day to coincide with thousands of others around the world. The data from all of these balloon is sent to the WMO and used in weather forecasting models. Upper level wind speeds are sent to aviation. An example of the data from 4 March 2023 is shown on the left.
|
Waves >>
Other Resources
|
PhET Simulation on the states of matter
|
|
PhET Simulation on the Gas Laws
|