Hannah Emmerson of Bermuda Sandcastle fame fire spinning on Southlands Beach (Photo: Chris Ingham)
7.1 - Moments, Torques and Couples
Objectives:
- To revise the concept of moments and torque
- To be able to calculate the torque about any given pivot
- To understand and be able to apply the principle of moments to solve static equilibrium problems
In the previous unit we looked at how balanced forces result in equilibrium – i.e. that if the forces up counteract the forces downwards etc then the object either doesn’t move or moves with a constant velocity. This is known as translational equilibrium. However, often forces act at a distance from a pivot (fulcrum) point. This can cause the object to rotate. The turning effect of this force is known as a turning moment or torque. An excellent understanding of torques is essential in architecture, engineering, biomechanics, set construction and sailing among many other fields.
It is easier to open a door if we push at the side furthest from the hinges, where the handle is. This is because the quantity that effects how easy it is to move the door in a rotational manner depends on a ‘torque’ or ‘moment’ and not a linear force.
In the UK we generally use the term ‘moment’ for the turning effect of a single force, and ‘torque’ for when the force is applied evenly around something like a shaft. The US tends to use the word ‘torque’ and ‘moment’ interchangeably. Therefore, for this unit we will use the US approach to maintain consistency with the exam and textbooks. In general we consider anti-clockwise torques are positive and clockwise torques are negative, although if you are careful with your diagrams and directions you can ignore the signs. (I do...). The equation uses "r" as the pivot is effectively the centre of the circle of rotation and the perpendicular distance is the radius. The cosine part is for when there is an angle different from 90 degrees between the force and the radius (later).
In the UK we generally use the term ‘moment’ for the turning effect of a single force, and ‘torque’ for when the force is applied evenly around something like a shaft. The US tends to use the word ‘torque’ and ‘moment’ interchangeably. Therefore, for this unit we will use the US approach to maintain consistency with the exam and textbooks. In general we consider anti-clockwise torques are positive and clockwise torques are negative, although if you are careful with your diagrams and directions you can ignore the signs. (I do...). The equation uses "r" as the pivot is effectively the centre of the circle of rotation and the perpendicular distance is the radius. The cosine part is for when there is an angle different from 90 degrees between the force and the radius (later).
\[Torque = Force \times{ perpendicular distance from the pivot}\]
\[\tau =Fr\cos \theta\]
For this topic we are generally interested in the conditions required for static equilibrium. Last unit we learned that if the forces up balanced the forces down as well as the forces left equalled the forces right an object is in static equilibrium. This is translational equilibirum. It can still rotate! For complete equilibrium the torques clockwise must counterbalance the torques anti-clockwise.
Two conditions for equilibrium:
\[\sum F=0\]
\[\sum \tau =0\]
\[\tau _{clockwise}=\tau _{anti-clockwise}\]
Two conditions for equilibrium:
\[\sum F=0\]
\[\sum \tau =0\]
\[\tau _{clockwise}=\tau _{anti-clockwise}\]
|
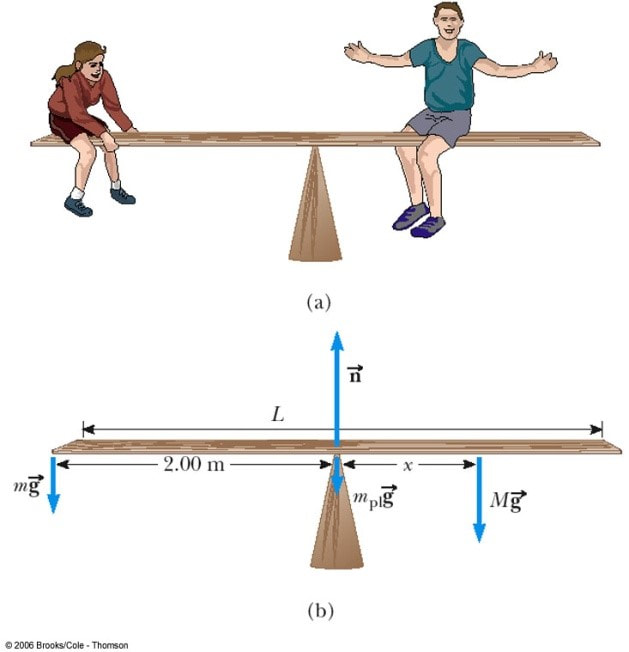
Example 1 (from College Physics): The total weight of the students downwards equals the normal force upwards at the pivot. We know this as the seesaw is in vertical equilibrium. There are no forces left or right to worry about.
\[F_{up}=F_{down}\] \[n=m_{plank}g+mg+Mg\] This leaves us with rotational equilibrium. If the torques clockwise and anti-clockwise about the pivot are equal, then the seesaw will not rotate and will be balanced. Note that the weight of the plank does not create a torque as it acts through the pivot. (its distance is zero)
\[\tau _{clockwise}=\tau _{anti-clockwise}\] \[2mg=Mg\times x\] \[x = \frac{2m}{M}\] |
The fun starts when the force is at an angle to the lever arm. The key here is remembering that the torque is related to the PERPENDICULAR distance from the pivot.
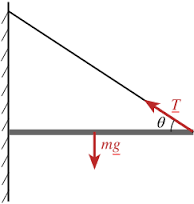
Example 1 - the classic balcony problem
This a basic set-up that is used frequently in structural engineering. If the support is from above it is known as a "tie" as it can be replaced by rope. If supported from below it is called a "strut". Taken further it is possible to use the concept of translational equilibrium to determine the forces on the wall. An AP question may ask what would be the effect of reducing the angle or sliding a box along the beam.
|
\[\tau _{clockwise}=\tau _{anti-clockwise}\]
\[mg\times \frac{l}{2}=T\sin \theta \times l\] \[T=\frac{mg}{2\sin \theta }\] |
|
Only just maintaining rotational equilibrium by a whisker.
|
|
BELCO pole in Somerset!
|
7.2 - Centre of Gravity and Complex Problems
Objectives:
|
When Isaac Newton started working on his theory of gravity, he realised that the total pull of gravity on an object was equal to the sum of the pulls on all its constituent parts (atoms). This hugely simplifies things. The total pull of gravity acts through the geometric centre of an object (of uniform density), which we call the centre of gravity (old school) or the centre of mass (modern). If the centre of gravity is not directly over the pivot it will exert a torque on the object. This needs to be included in to the situation.
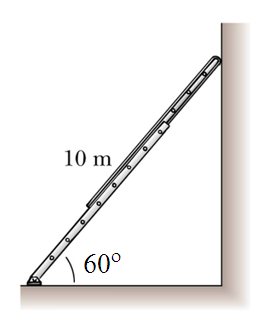
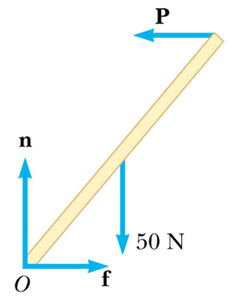
Example 2 - the classic ladder problem
|
|
We often use ladders at BMDS to work up on the lighting grid and at boatyards. It is vitally important that tall ladders have someone at the bottom to stop the bottom of the ladder slipping away from the wall. Effectively, the only thing stopping the ladder falling is the frictional force on the ground, f.
Step 1 - vertical equilibrium:
\[F_{up}=F_{down}\]
\[n = 50\,\text{N}
Step 2 - horizontal equilibrium:
\[F_{left}=F_{right}\]
\[f = P = \mu n=50\mu\]
\[F_{left}=F_{right}\]
\[f = P = \mu n=50\mu\]
Step 3 - rotational equilibrium about base:
\[\tau _{clockwise}=\tau _{anti-clockwise}\]
\[\left ( 50 \cos 60^{\circ}\right )\times \frac{10}{2}=\left ( P\cos 30^{\circ} \right )\times 10\]
\[\left ( \cos 60^{\circ}\right )=2\left ( \mu \cos 30^{\circ} \right )\]
\[\mu =\frac{\cos 60^{\circ}}{2\cos 30^{\circ}}=\frac{1}{2\sqrt{3}}=0.29\]
\[\tau _{clockwise}=\tau _{anti-clockwise}\]
\[\left ( 50 \cos 60^{\circ}\right )\times \frac{10}{2}=\left ( P\cos 30^{\circ} \right )\times 10\]
\[\left ( \cos 60^{\circ}\right )=2\left ( \mu \cos 30^{\circ} \right )\]
\[\mu =\frac{\cos 60^{\circ}}{2\cos 30^{\circ}}=\frac{1}{2\sqrt{3}}=0.29\]
AP-style question: Describe what happens to the frictional force as someone starts to climb up the ladder.
YouTube video of the capsize of the 70' trimaran Spindrift. An example of the turning moment of the sails exceeding that of the weight of the hull. Once the weight is beyond the pivot point, in this case the port pontoon, then a capsize is inevitable.
|
A car ship abandoned in the Bay of Biscay Jan 2016
|
|
Hoisting a mast into a sail boat at the RBYC Sept 2017. The lifting point is not at the centre of mass so an extra force needs to be applied at the lower end.
|
|
|
AC75 - this the brand-new (21 Nov 2017) concept for the next America's Cup Race. This is a complicated piece of physics.
|