4.1 - Wave Motion
Objectives:
- Be able to quantify the period, frequency, speed, wavelength and height of a wave.
- Understand that wave motion transfers energy without transferring matter.
- Understand that wave involve a circulating motion that extends below the surface.
- Understand the effect that current has on waves.
- Know the effect the waves has on a moving boat.
Waves are a defining characteristic of the sea. They are regular and repetitive motion of the water at the surface. There are 5 main types of waves found on the ocean:
- ripples (or capillary waves)
- wind driven waves
- swell
- tsunamis
- tides
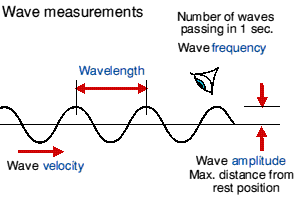
The generic wave form found in physics is useful for visualising the features and variables of any wave. It is important to be conversant with the terms: period, frequency, wavelength, wave speed and wave height. The period is the time interval between successive crests and can range from 1/100th of a second to just over a day. Wave period off South Shore can easily be measured by timing the period off 10 successive waves and dividing the answer by 10.
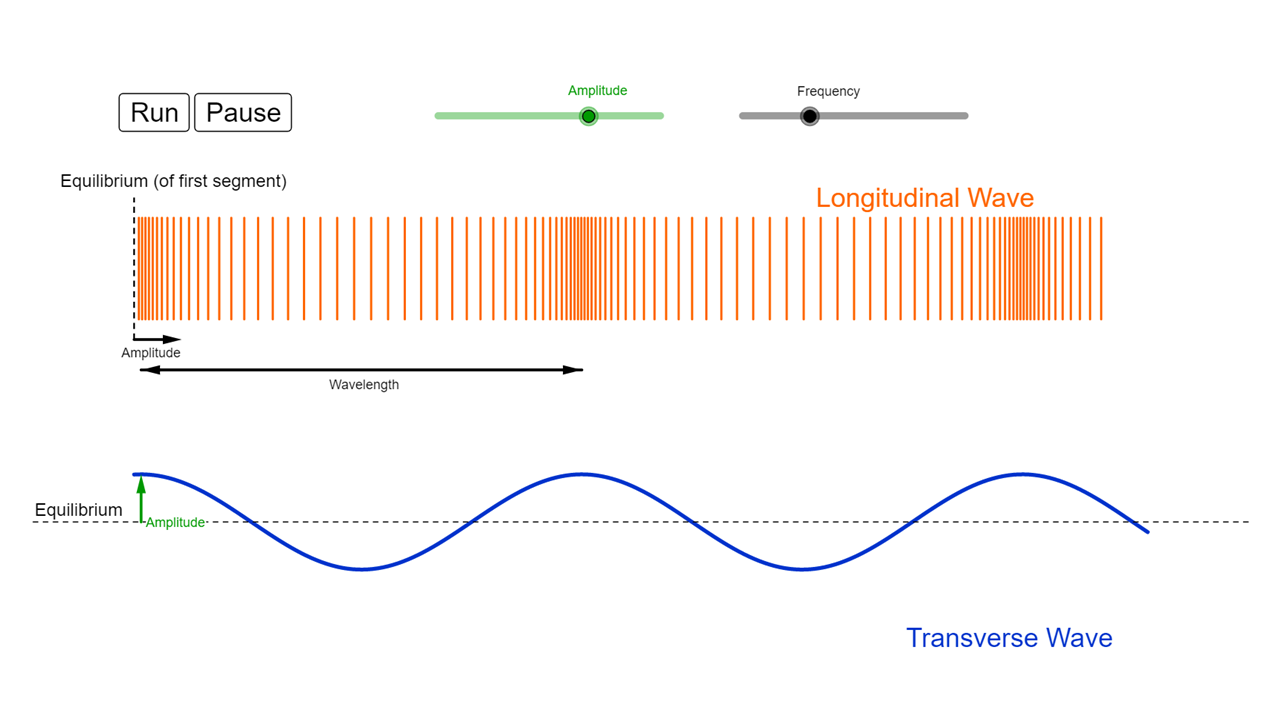
However, only the smallest ripples on a calm sea look like the sinusoidal wave shown above. Surface tension and gravity affect its shape and the wave becomes more angular and steeper as the driving force (wind) increases. The actual motion of the water molecules is not straight up and down as the slinky spring model would suggest, but rather they move in circles, slowly progressing in the direction of the wave. This circular motion affects the water below it and starts more moving in circles deeper underwater. The overall wave motion can continue underwater for \(5\) circles of decreasing magnitude - to a depth of approximately \(\frac{1}{2} \times wavelength\).
If the wave height gets too high, the steepness of the front of the wave can exceed \(120^{\circ}\) - when the height exceeds \(\frac{1}{7} \lambda\) - and the top of the wave collapses, and/or gets blown off by the wind. If small scale (usually \(12 - 15 \,\text{kts}\) of wind), these are called "white caps". If larger, they go by the rather romantic "white horses".
The speed of a water wave depends on the wavelength. The longer the wavelength, the faster the wave. The equation that relates these variables is:
\[v=\sqrt{\frac{g \lambda}{2 \pi}}\]
which simplifies to:
\[v=1.25\sqrt{\lambda}\]
In knots the approximate formula is easiest if related to the period, \(T\):
\[v=1.5 \times T\]
If the wave height gets too high, the steepness of the front of the wave can exceed \(120^{\circ}\) - when the height exceeds \(\frac{1}{7} \lambda\) - and the top of the wave collapses, and/or gets blown off by the wind. If small scale (usually \(12 - 15 \,\text{kts}\) of wind), these are called "white caps". If larger, they go by the rather romantic "white horses".
The speed of a water wave depends on the wavelength. The longer the wavelength, the faster the wave. The equation that relates these variables is:
\[v=\sqrt{\frac{g \lambda}{2 \pi}}\]
which simplifies to:
\[v=1.25\sqrt{\lambda}\]
In knots the approximate formula is easiest if related to the period, \(T\):
\[v=1.5 \times T\]
This changes as the wave moves into shallower water. As the wave motion extends down to approximately half of its wavelength, if the depth is less than this the wave will be affected by the seabed. This has the effect of slowing the wave down. As the period of the wave is unchanged, this has the effect of reducing the wavelength. The wave gets shorter and steeper. It is more likely to exceed 1/7th of its wavelength and break. As it gets close inshore into very shallow water the rolling motion itself is affected and the wave tumbles - this is surf. The approximate speed of a shallow water wave is given by:
\[v = \sqrt{gd}\]
Extremely long wavelength waves (tsunamis and tides) will always be classified as 'shallow water waves' as the depth of the ocean is always less than half their wavelength.
In a given area, waves are produced of different wavelengths. The longer wavelength travel faster than the shorter wavelengths. It is possible that the longer ones travel fast enough to leave the area of disturbance and become swell.
\[v = \sqrt{gd}\]
Extremely long wavelength waves (tsunamis and tides) will always be classified as 'shallow water waves' as the depth of the ocean is always less than half their wavelength.
In a given area, waves are produced of different wavelengths. The longer wavelength travel faster than the shorter wavelengths. It is possible that the longer ones travel fast enough to leave the area of disturbance and become swell.
|
OPhysics - this is a nice simulation of a transverse wave, which is what the ocean waves are. The longtail view from the top appears as a longitudinal wave.
Real water waves are not these perfect sinusoidal shape, but this does show the relationships between frequency, period and wave speed as well as the amplitude. Note that wave height as measured by mariners is twice the amplitude. |
Animation of non-breaking waves at sea. Image from Dan Russell - click image to view original page.
|
|
|
Diffraction
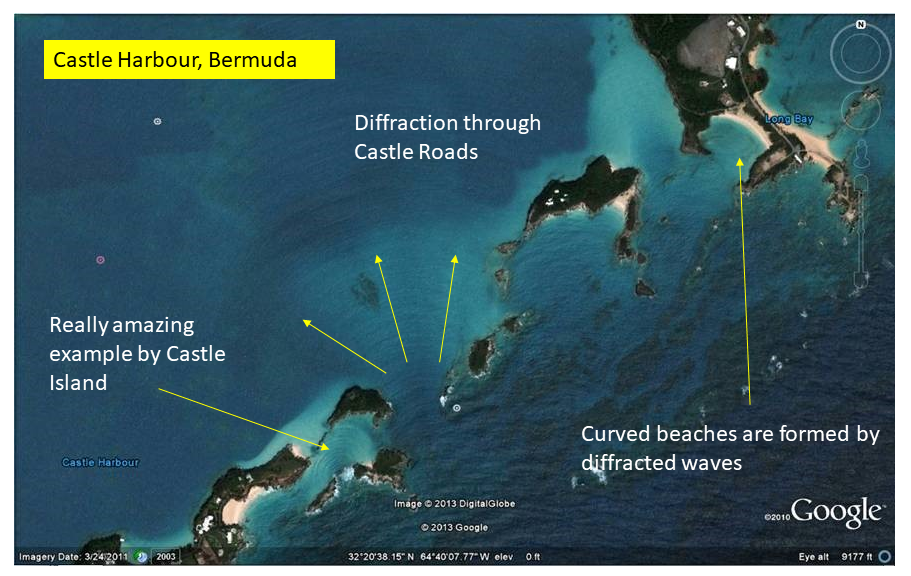
All waves in physics diffract (spread out) as they pass through a gap. This is very common when sea waves meet islands, gaps in a reef, harbour entrances, and headlands. As the gap size decreases the curvature of the wave increases. When the gap size is about the same as the wavelength, the resulting curvature is essentially circular. There are some interesting consequences of diffraction. Curved beaches like Horseshoe Bay are formed. Swell diffracting around a headland can cause the swell to be striking an anchored boat on the beam, causing it to roll. Scanning over Bermuda on Google Earth can usually show up many examples of diffraction - the best are usually around the entrance to Castle Harbour - see photo.
All waves in physics diffract (spread out) as they pass through a gap. This is very common when sea waves meet islands, gaps in a reef, harbour entrances, and headlands. As the gap size decreases the curvature of the wave increases. When the gap size is about the same as the wavelength, the resulting curvature is essentially circular. There are some interesting consequences of diffraction. Curved beaches like Horseshoe Bay are formed. Swell diffracting around a headland can cause the swell to be striking an anchored boat on the beam, causing it to roll. Scanning over Bermuda on Google Earth can usually show up many examples of diffraction - the best are usually around the entrance to Castle Harbour - see photo.
Screenshot from a PhET simulation showing the diffraction of waves through a gap in a harbour wall. Clicking the image will lead to the simulation and you can experiment with changing the gap size and the wavelength. We can also demonstrate this effect with the ripple tank in the lab.
Interference
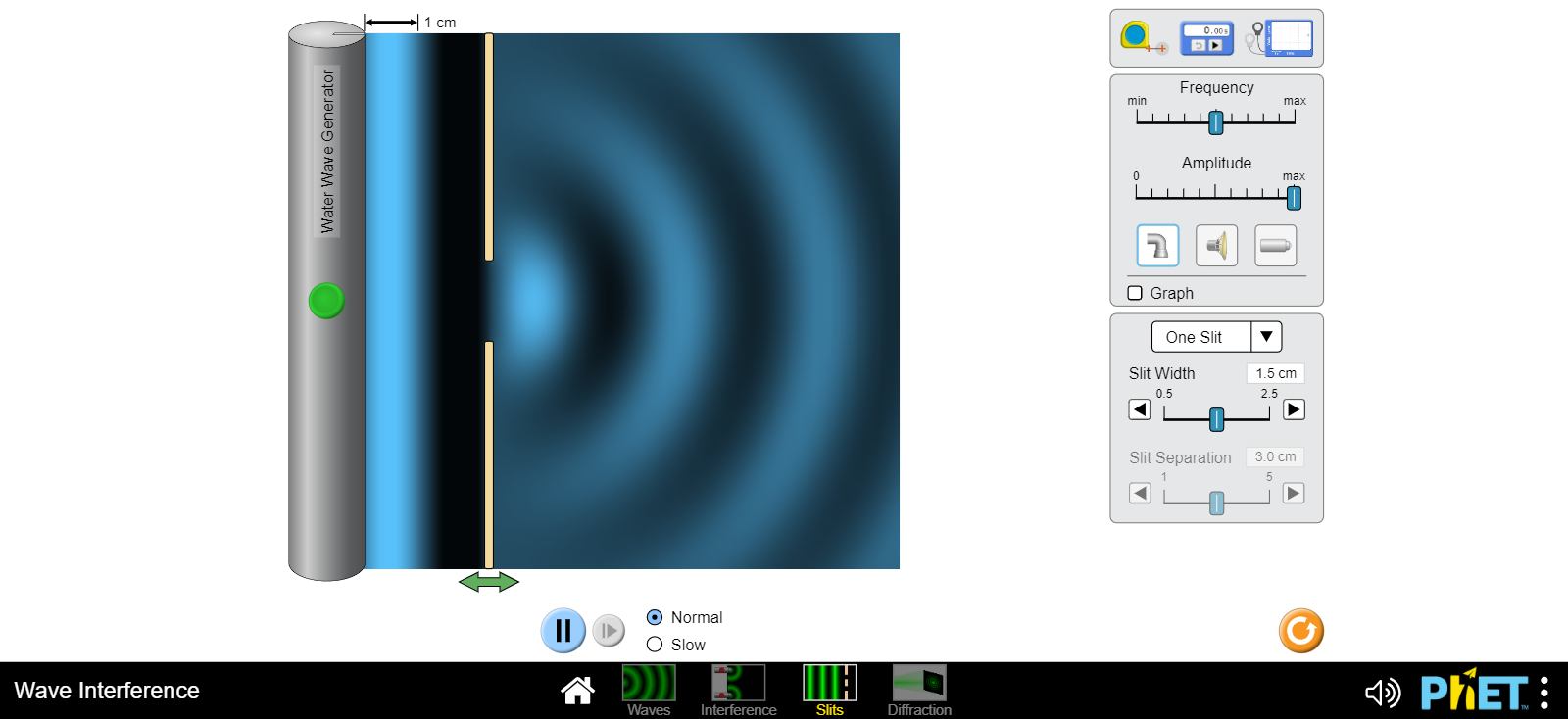
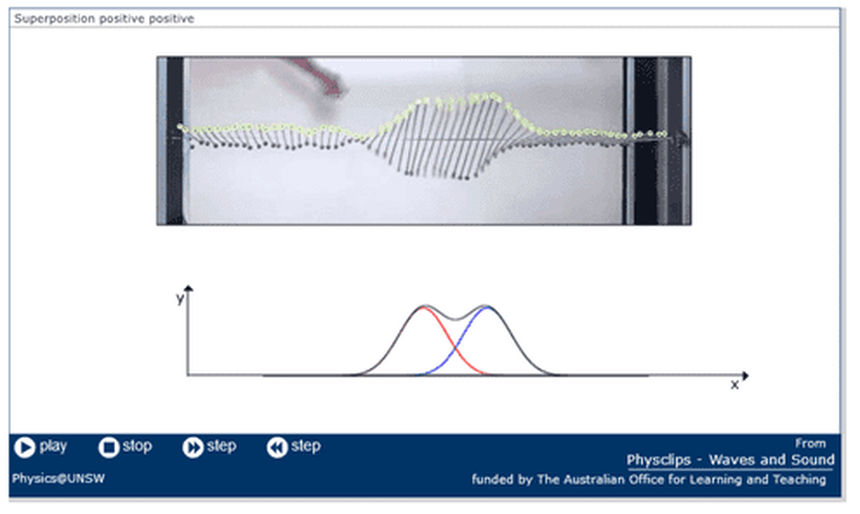
Interference occurs when two waves meet. The two crests combine to form a much larger wave. After this, the two waves continue on their respective waves as if nothing had ever happened. On the ocean, this is commonly seen when a swell from a distant storm is overlaid with locally produced wind driven waves. The waves are superimposed over the swell - occasionally leading to some really big waves. If the swell and the waves are moving in different directions, especially if not parallel, but at an angle, then we get what sailors call a confused sea.
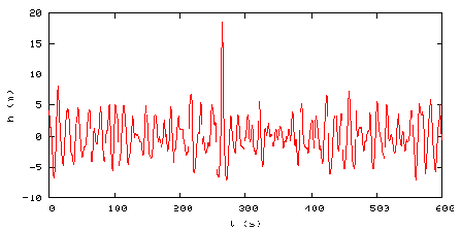
The superposition of two waves can lead to Rogue Waves, which were mythical for a long time - mainly as anyone who came across one rarely lived to tell the tale - but have since been recorded. There was a particularly spectacular example called the Draupner Wave that was recorded by the Draupner Oil Platform in the North Sea during a storm in 1995. There was one wave that was almost twice the height of the other waves.
Interference occurs when two waves meet. The two crests combine to form a much larger wave. After this, the two waves continue on their respective waves as if nothing had ever happened. On the ocean, this is commonly seen when a swell from a distant storm is overlaid with locally produced wind driven waves. The waves are superimposed over the swell - occasionally leading to some really big waves. If the swell and the waves are moving in different directions, especially if not parallel, but at an angle, then we get what sailors call a confused sea.
The superposition of two waves can lead to Rogue Waves, which were mythical for a long time - mainly as anyone who came across one rarely lived to tell the tale - but have since been recorded. There was a particularly spectacular example called the Draupner Wave that was recorded by the Draupner Oil Platform in the North Sea during a storm in 1995. There was one wave that was almost twice the height of the other waves.
Screenshot of a video/animation showing the superposition of waves. Clicking will lead a whole page about physics waves, scrolling down will lead to this example.
|
Data from the Draupner Wave - source Wikipedia. Clicking the image will take you to the webpage.
|
|
|
|
|
|
OC 4.1 - Wave Motion
Revision video made during the COVID lockdown spring 2020. Audio quality is poor due to terrible laptop mic. |
ACTIVITIES
As every one in Bermuda lives less than a mile from the sea, we see it every day. Waves are almost always present on the surface of the water. A great activity is to go to the sea and observe these waves with a scientist's mind.
|
OC 4.1 - Wave Properties
|
| ||
|
OC 4.2 - Watching Waves. An out-of-school task to go to the beach and look at waves!
|
| ||
|
Powerpoint produced for online lecture, Dec 2020
|
| ||