|
Thermal Physics is the science behind heat and temperature. This affects everything about our lives; for example - the time taken for Mrs Paynter to freeze 400 popsicles, the amount of energy and hence money used to air condition the school, the efficiency of your bike engine, why soda feels refreshing to drink, why it hurts to hold your breath under water to how the weather and climate systems work, and even the thermal processes within the Sun!
|
2.1 - Heat and Temperature
Objectives:
- Appreciate the difference between heat and temperature
- Understand the concept of thermal equilibrium
- Know that the measurement of temperature involves a variable response time
Heat and temperature are NOT the same thing! Things are hot because the particles that they are made from are moving and hence have kinetic energy. Heat is a measure of the transfer of energy between objects and temperature is a measure of how hot it is – or a measure of the average speed of the particles that that it is made of. The temperature of a body can be defined as the degree of hotness or coldness of a body. Temperature can only tell us how hot or cold an object is and not the amount of energy it contains. A spark hitting your skin that is at a temperature of thousands of degrees will not hurt anywhere near as much as a cup of boiling water.
Heat = transfer of energy between objects
Temp = mean value of the KE of the particles
Temp = mean value of the KE of the particles
Thermometry
Measuring temperature is far easier than measuring the heat content of a substance, although not altogether trivial. Students have been measuring temperature with thermometers for years at school, usually without really understanding what they are doing! A standard alcohol thermometer works by thermal expansion, as the alcohol molecules gain KE they move faster and tend to spread out more. For temperatures between about \(-10 \rightarrow 110^{\circ} \text{C}\) this expansion is close to linear. Add a dye to the alcohol and a calibrated scale and voila, you have a reasonably accurate thermometer. The biggest error with this is that it takes TIME (called the response time) for the the heat from the surrounding substance to get to/from the thermometer. The reading is only really accurate if the alcohol is at the same temperature as the substance being measured, and all the alcohol, not just the stuff in the bulb at the bottom. Mercury thermometers have a more linear rate of expansion and a shorter response time, so are more accurate. However, students tend to break them and mercury is rather toxic. Other issues with the cheap alcohol thermometers are: they are mass produced so the scales are not terribly accurately applied and naughty students often put them in a flame, which creates bubbles in the thread. Better thermometers are the electronic ones that we use with the data loggers. These are based on thermocouples.
Measuring temperature accurately in a situation where the temperature is changing rapidly is a major problem in science. Some examples in Bermuda are: the twice daily weather balloon that is measuring the temperature and humidity profile of the atmosphere, divers measuring the temperature profile of the sea.
Measuring temperature is far easier than measuring the heat content of a substance, although not altogether trivial. Students have been measuring temperature with thermometers for years at school, usually without really understanding what they are doing! A standard alcohol thermometer works by thermal expansion, as the alcohol molecules gain KE they move faster and tend to spread out more. For temperatures between about \(-10 \rightarrow 110^{\circ} \text{C}\) this expansion is close to linear. Add a dye to the alcohol and a calibrated scale and voila, you have a reasonably accurate thermometer. The biggest error with this is that it takes TIME (called the response time) for the the heat from the surrounding substance to get to/from the thermometer. The reading is only really accurate if the alcohol is at the same temperature as the substance being measured, and all the alcohol, not just the stuff in the bulb at the bottom. Mercury thermometers have a more linear rate of expansion and a shorter response time, so are more accurate. However, students tend to break them and mercury is rather toxic. Other issues with the cheap alcohol thermometers are: they are mass produced so the scales are not terribly accurately applied and naughty students often put them in a flame, which creates bubbles in the thread. Better thermometers are the electronic ones that we use with the data loggers. These are based on thermocouples.
Measuring temperature accurately in a situation where the temperature is changing rapidly is a major problem in science. Some examples in Bermuda are: the twice daily weather balloon that is measuring the temperature and humidity profile of the atmosphere, divers measuring the temperature profile of the sea.
Temperature Scales
When Gabriel Fahrenheit invented the mercury thermometer he needed to create a temperature scale to standardize it. After all, simply saying that something was cold, warm or hot wasn't very scientific. In the absence of anything else and bearing in mind that so many systems of measurement were simply dreamt up out of thin air (feet, inches, pounds etc), he devised what he called the Fahrenheit Scale. He based the zero point at the melting point of a saturated ammonium chloride solution as he figured that this was easily replicated and colder than most temperatures naturally experienced (never been to Canada...) and the \(100^{\circ} \text{F}\) point at the body temperature of a horse as it was more stable than a human's. This worked fine (and still in use in Bermuda and the US), but has since been superseded by Anders Celsius' centigrade scale based on the freezing and boiling points of pure water. Strictly speaking degrees centigrade is not exactly the same as degrees Celsius. A centigrade scale takes the 0 and the 100 points and linearly divides them into a 100 degrees. It assumes that the expansion rate of the measuring fluid is perfectly linear... In practical terms this difference is so small as to be negligible.
BUT - in physics terms, both the Fahrenheit and Celsius scales are fundamentally flawed as they are based on arbitrary zero points and hence can have values of less than 0. The definition of temperature is the mean KE of the moving particles. This can never be less than zero. The coldest possible temperature therefore must be when all atomic motion stops completely and the mean \(KE = 0\). This demands an ABSOLUTE temperature scale where absolute zero = zero. The simplest solution for scientists was to determine what temperature absolute zero was and then re-zero the existing Celsius scale to match it. That way normal people could carry on using their thermometers and Celsius scales and the scientists can use re-jigged one. This is called the Kelvin scale after Lord Kelvin. Conversion is easy - just add or subtract \(273.15^{\circ}\).
Note 1: strictly speaking, the Celsius scale measures temperature difference - i.e. the difference between the temperature of an object and the melting point of pure water. It uses degrees. So the temperature of the ocean in August is 32 degrees C. However, the Kelvin scale is absolute, so we don't use the word "degrees". We simply say that the boiling point of He-3 is 4.2 K.
Note 2: there is an absolute version of the Fahrenheit scale, called the Rankin scale - but no one ever uses it
BUT - in physics terms, both the Fahrenheit and Celsius scales are fundamentally flawed as they are based on arbitrary zero points and hence can have values of less than 0. The definition of temperature is the mean KE of the moving particles. This can never be less than zero. The coldest possible temperature therefore must be when all atomic motion stops completely and the mean \(KE = 0\). This demands an ABSOLUTE temperature scale where absolute zero = zero. The simplest solution for scientists was to determine what temperature absolute zero was and then re-zero the existing Celsius scale to match it. That way normal people could carry on using their thermometers and Celsius scales and the scientists can use re-jigged one. This is called the Kelvin scale after Lord Kelvin. Conversion is easy - just add or subtract \(273.15^{\circ}\).
Note 1: strictly speaking, the Celsius scale measures temperature difference - i.e. the difference between the temperature of an object and the melting point of pure water. It uses degrees. So the temperature of the ocean in August is 32 degrees C. However, the Kelvin scale is absolute, so we don't use the word "degrees". We simply say that the boiling point of He-3 is 4.2 K.
Note 2: there is an absolute version of the Fahrenheit scale, called the Rankin scale - but no one ever uses it
2.2 - Heat Transfer
Objectives:
- To understand the three main methods of heat transfer; conduction, convection and radiation.
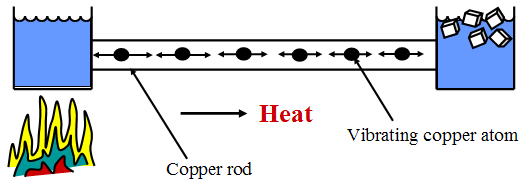
Conduction
Conduction is the process where heat energy flows from hotter regions to colder regions without any net movement of the substance. In non-metallic solids this is the result of interactions between neighbouring atoms and molecules randomly colliding. The hot end of a material has rapidly vibrating particles that in turn pass on their vibrational energy to their neighbouring particles. This process works best in metallic solids. Poor conductors of heat are called insulators. Liquids and gases tend to be very poor conductors.
Convection
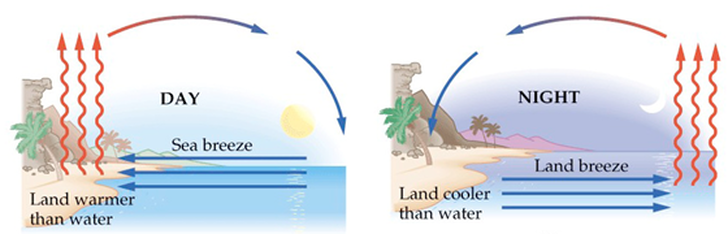
Convection is the principle method of heat transfer in fluids (liquids and gases). It is the method that is responsible for driving the climate system on Earth. The basic idea is straightforward and covered at IGCSE. The warmer fluid has particles that are moving faster, therefore they tend to spread apart more. This makes that section of the fluid less dense and hence buoyant. The warm fluid rises and is replaced by a cooler fluid. If there is a consistent heat source and enough space, this sets up a continuous movement of the fluid called a convection current. This leads to wind and ocean currents! There are a large number of demonstrations of this in your physics class. The maths of convection is horribly complicated and not expected at AP level. As a sailor, I often experience a sea breeze. This is a early afternoon wind that can form at the coast if two conditions are met: a) the gradient winds caused by large scale systems are not present and b) there is thermal heating of the land such that the land becomes warmer than the sea. A large regatta every August in Cowes, UK, frequently depends on a sea breeze filling in!
|
The diagram above shows the formation of a sea breeze and its counterpoint, the land breeze. What is missing off the diagram is that the rising air usually causes fluffy cumulus clouds to form, which in Bermuda are known as Morgan's Cloud (photo). Photo below shows sea breeze clouds building on the mainland shore of the Solent, UK
|
Radiation
Thermal radiation is an electromagnetic wave that is emitted by any object that has a temperature above absolute zero. As such it can travel through a vacuum and moves at the speed of light. A key variable is the wavelength (or frequency) of this wave. For most everyday objects it is in the Infrared (IR) part of the spectrum. The hotter the object, the higher the frequency of the wave. If an object is hot enough, then this radiation becomes visible (red-hot). This colour change is a method used to measure the temperature of stars! Blue stars are far hotter than red stars. Our Sun emits predominantly yellow light. As everyone who lives in the tropics knows; black surfaces absorb more thermal radiation than white or silvered surfaces. What is almost counterintuitive is that black surfaces also emit that radiation faster as well. You are not expected to be able to solve numerical problems on this.
|
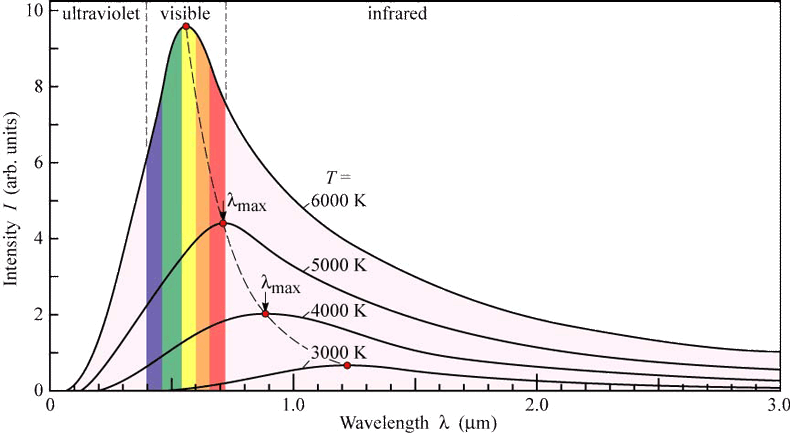
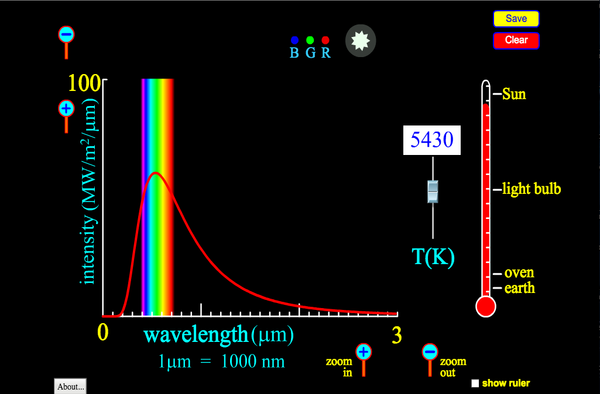
A curve showing the thermal radiation emitted from the Sun. The majority of the radiation is in the visible part of the spectrum - i.e. we can it! As the temperature gets cooler, the mean wavelength increases and we can no longer see it, but still feel the infrared as warmth.
(This is the so-called "Blackbody Spectrum") |
2.3 - Specific and Latent Heat Capacities
Objectives:
- Be able to calculate the energy or time required to heat or cool an object
- Be able to calculate the energy or time required to change the state of a substance
If we heat an object its temperature increases until it reaches its boiling point. Then the energy is purely going into the change of state and the temperature remains the same.
Specific Heat
When we add heat energy to an object, its temperature increases. Conversely, to cool down something we need to remove heat energy from it. The amount of heat needed to change the temperature of something rather depends on how big it it and what it is. The "what it is" is known officially as it "specific heat capacity" and it is a complicated function based on atomic mass, bonding strength, density etc. We ignore all that and define it as how much heat energy is required to heat \(1.0 \text{kg}\) of it by \(1.0^{\circ} \text{C}\). The only value that I ever remember is that of water as it is a) common and b) super important in experimental work in biology, chemistry and physics! \(c = 4200 \text{J/kgK}\).
The equation for this is:
\[Q=mc\Delta T\]
The equation for this is:
\[Q=mc\Delta T\]
You have probably used this equation in science before – usually when you burn food under a test tube of water to measure the energy content of the various food groups. It must be noted that this equation breaks down during the change of state, so only works during one phase (e.g. liquid) The specific heat of a substance varies a great deal. A large part of the world’s climate system can be explained by the differing heat capacities of air, water and land! You may have noticed the changing temperatures of the beach and ocean during the diurnal cycle. At night the beach is cold and the ocean warm, during the day the beach is hot and the ocean still only warm! The specific heat capacity of water is very high. It takes about \(4200 \text{J}\) of heat energy to raise the temperature of a \(1 \text{kg}\) mass by \(1^{\circ} \text{C}\). Incidentally, this is the definition of the Calorie (kCal)
Latent Heat
While the state of a substance is changing, e.g. water is boiling, heat energy is still being supplied but the temperature does not increase. The energy is going into breaking the bonds and changing state. As this heat energy appears to be hidden as the temperature does not rise, it is known as “latent” heat. If the state is between a solid and a liquid we use the term “latent heat of fusion” and for the liquid to gas change “latent heat of vaporisation”. These latent heat values can be huge. There is a lot more energy in steam than hot water!
The equation is somewhat simpler, where \(L\) = specific latent heat.
\[Q=mL\]
The equation is somewhat simpler, where \(L\) = specific latent heat.
\[Q=mL\]
The latent heat can be rather large. e.g. for water --> steam, it is about \(2.0 \times 10^{6} \,\text{J/kg}\).
LAB WORK - a standard practical exercise for this is to pour exactly \(1.0 \,\text{kg}\) of water into a kettle that does not automatically switch off. Students determine how long it will take to boil based on the power rating (usually \(1500\, \text{W}\) ). Then if left to boil for \(5\,\text{mins}\), students can calculate the amount of water left in the kettle. Compare the values achieved with the theoretical ones and discuss the potential sources of error.
2.4 - The Gas Laws
Objectives:
- To know and understand the three gas laws – including lab-based work.
- To be able to use the Universal Gas Law equation
- To learn the ideal gas equation, \(pV = nRT\)
The gas laws are super important, a) they are routinely featured in AP exams, b) without a solid understanding of them the topic of heat engines is a non-starter and c) they are surprisingly relevant in everyday life – so there! Luckily for all concerned, you have met three of them before at IGCSE and in AP Chemistry and besides, they are pretty straightforward…
In any given fixed mass of gas there are only THREE macroscopic variables that can be easily measured.
In any given fixed mass of gas there are only THREE macroscopic variables that can be easily measured.
In science, life is a lot simpler if we only change one variable at a time. This is what the discoverers of the Gas Laws did too. They each fixed one of the three variables and worked on the relationship between the other two. This led to three gas laws – one for each fixed variable. They are:
NOTE: The temperature variable MUST ALWAYS be expressed in KELVINS – no exceptions!
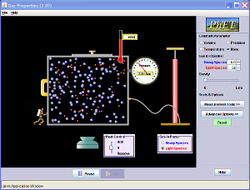
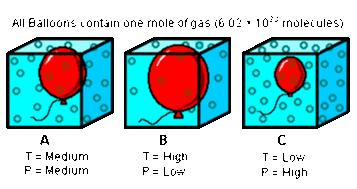
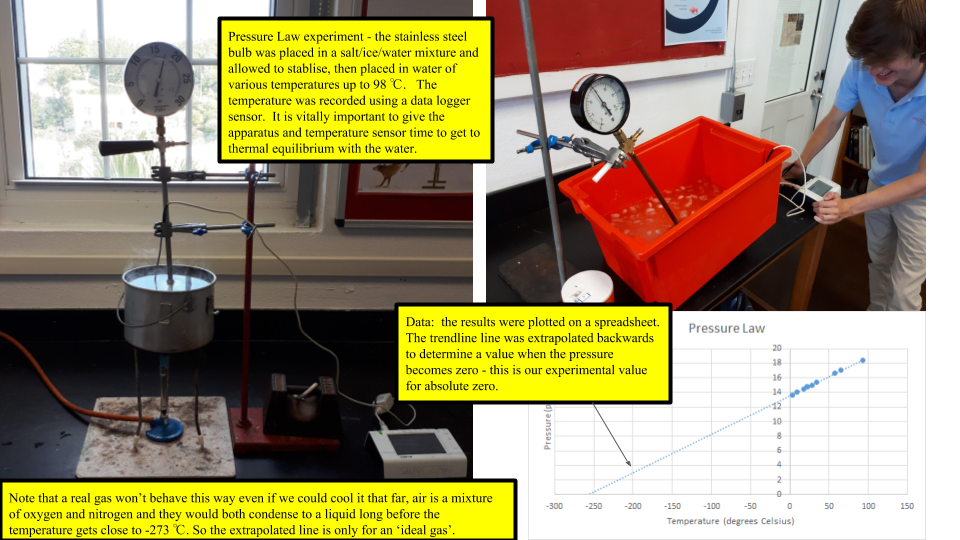
Pressure Law
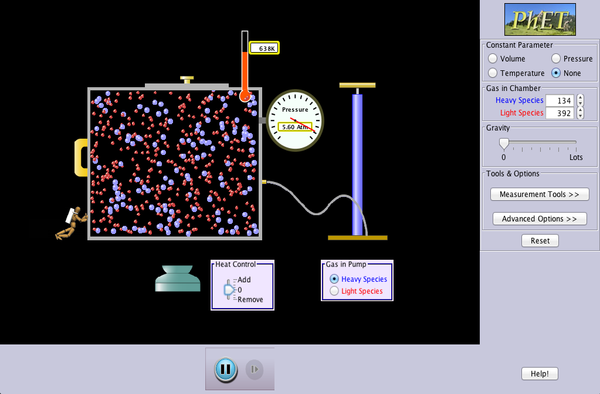
The pressure law is one of the three macroscopic gas laws; it states that for a fixed mass of gas with a constant volume: pressure/temperature is constant. As the gas inside the box is heated the temperature increases. This means that the particles are moving faster, so there is less time between collisions of the walls of the container. This will result in more collisions per second which in turn means a greater force, hence a greater pressure. "Heat a gas, its pressure increases"
\[\frac{P_{1}}{T_{1}}= \frac{P_{2}}{T_{2}}\]
- Pressure Law (V fixed)
- Charles’ Law (P fixed)
- Boyle’s Law (T fixed)
NOTE: The temperature variable MUST ALWAYS be expressed in KELVINS – no exceptions!
Pressure Law
The pressure law is one of the three macroscopic gas laws; it states that for a fixed mass of gas with a constant volume: pressure/temperature is constant. As the gas inside the box is heated the temperature increases. This means that the particles are moving faster, so there is less time between collisions of the walls of the container. This will result in more collisions per second which in turn means a greater force, hence a greater pressure. "Heat a gas, its pressure increases"
\[\frac{P_{1}}{T_{1}}= \frac{P_{2}}{T_{2}}\]
Popcorn Physics - why does popcorn pop?
Popcorn is the seed of the corn plant, similar to sweetcorn. Usually it is dried shortly after harvesting and can be stored for many years, and thus is a valuable agricultural commodity. It is starch-rich and scientists and food companies have found a vast amount of use for it. In its popcorn form it consists of a small kernel (which is the bit that starts the new plant), a large amount of starchy endosperm (which fuels the growth until the leaves appear) and a hard outer case. In the natural world, this outer case must be broken down to allow water to get to the inside to trigger germination. Humans have a much more exciting method... The endosperm is pretty dry but still contains about 14% water. When this is heated, the water boils and vaporises to form steam. The outer casing can withstand this for a period of time, but as more and more steam is produced, the pressure increases and increases until the casing can no longer withstand it. When it fails, it fails explosively, blown roughly equally in all directions. As the endosperm is riddled with water vapour bubbles that have been super-heated under pressure, the starch is instantly cooked as the casing fails and the water vapour is free to expand. Result - styrofoam-like popcorn! The expansion of the casing is fast enough to trigger a shockwave in the air - pop. Surprisingly, apparently the microwaves from cell phones are enough to trigger the cooking process. Caveat: haven't tried this myself yet.
Popcorn is the seed of the corn plant, similar to sweetcorn. Usually it is dried shortly after harvesting and can be stored for many years, and thus is a valuable agricultural commodity. It is starch-rich and scientists and food companies have found a vast amount of use for it. In its popcorn form it consists of a small kernel (which is the bit that starts the new plant), a large amount of starchy endosperm (which fuels the growth until the leaves appear) and a hard outer case. In the natural world, this outer case must be broken down to allow water to get to the inside to trigger germination. Humans have a much more exciting method... The endosperm is pretty dry but still contains about 14% water. When this is heated, the water boils and vaporises to form steam. The outer casing can withstand this for a period of time, but as more and more steam is produced, the pressure increases and increases until the casing can no longer withstand it. When it fails, it fails explosively, blown roughly equally in all directions. As the endosperm is riddled with water vapour bubbles that have been super-heated under pressure, the starch is instantly cooked as the casing fails and the water vapour is free to expand. Result - styrofoam-like popcorn! The expansion of the casing is fast enough to trigger a shockwave in the air - pop. Surprisingly, apparently the microwaves from cell phones are enough to trigger the cooking process. Caveat: haven't tried this myself yet.
|
|
Five cell phones are rung to trigger the popcorn!
|
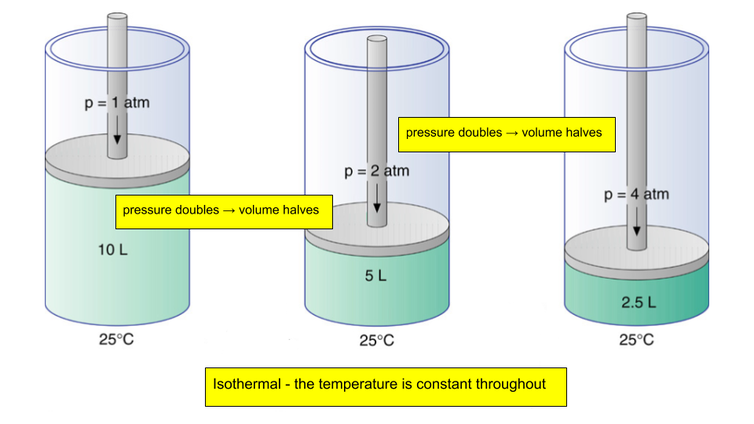
Boyle's Law
Boyle’s law is one of the three macroscopic gas laws; it states that for a fixed mass of gas at a constant temperature. When the volume is halved the pressure doubles. In theory the temperature of the gas does not change, this is an isothermal process. If the temperature is the same then the kinetic energy of the particles is the same, which means that their average speed remains the same. In a smaller volume there is less time between collisions of the particles and the walls of the container. More collisions means more forces are exerted, this results in a greater pressure.
Bermuda relevance: scuba diving! "Use pressure to squash a gas, it gets smaller"
\[{P_{1}V_{1}}= {P_{2}V_{2}}\]
Boyle’s law is one of the three macroscopic gas laws; it states that for a fixed mass of gas at a constant temperature. When the volume is halved the pressure doubles. In theory the temperature of the gas does not change, this is an isothermal process. If the temperature is the same then the kinetic energy of the particles is the same, which means that their average speed remains the same. In a smaller volume there is less time between collisions of the particles and the walls of the container. More collisions means more forces are exerted, this results in a greater pressure.
Bermuda relevance: scuba diving! "Use pressure to squash a gas, it gets smaller"
\[{P_{1}V_{1}}= {P_{2}V_{2}}\]
|
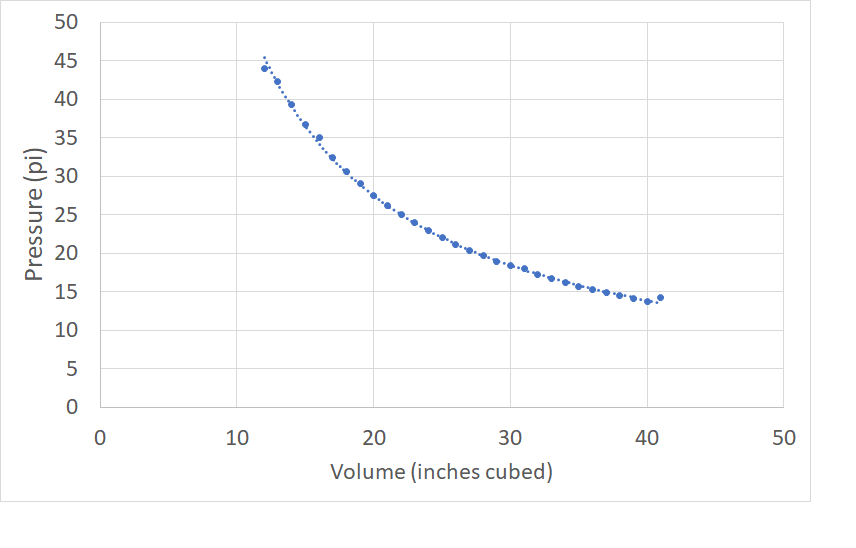
Lab Demonstration
We use the following apparatus to demonstrate quantitatively the relationship between the applied pressure and the volume of the trapped gas. Our apparatus is pretty dated, but still works. The units are psi and cubic inches, but the results are usually pretty good. This is a useful exercise in linearising data. |
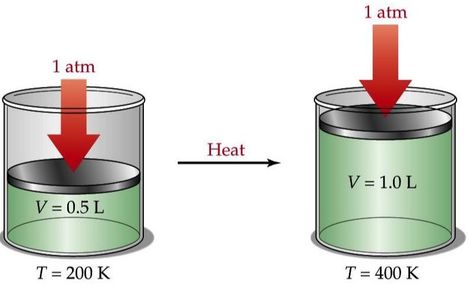
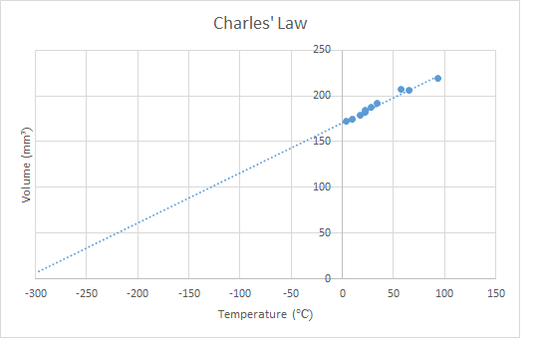
Charles' Law
This law states that for a fixed mass of gas at a constant pressure. As the temperature of a gas increases, the particles move faster, if the gas is free to expand, then the volume increases in proportion to the absolute temperature. "Heat a gas, it expands"
\[\frac{V_{1}}{T_{1}}= \frac{V_{2}}{T_{2}}\]
This law states that for a fixed mass of gas at a constant pressure. As the temperature of a gas increases, the particles move faster, if the gas is free to expand, then the volume increases in proportion to the absolute temperature. "Heat a gas, it expands"
\[\frac{V_{1}}{T_{1}}= \frac{V_{2}}{T_{2}}\]
Swipe Diagram: based on the PhET simulation "Gas Laws"
|
Image (temp until I take a photo of ours)
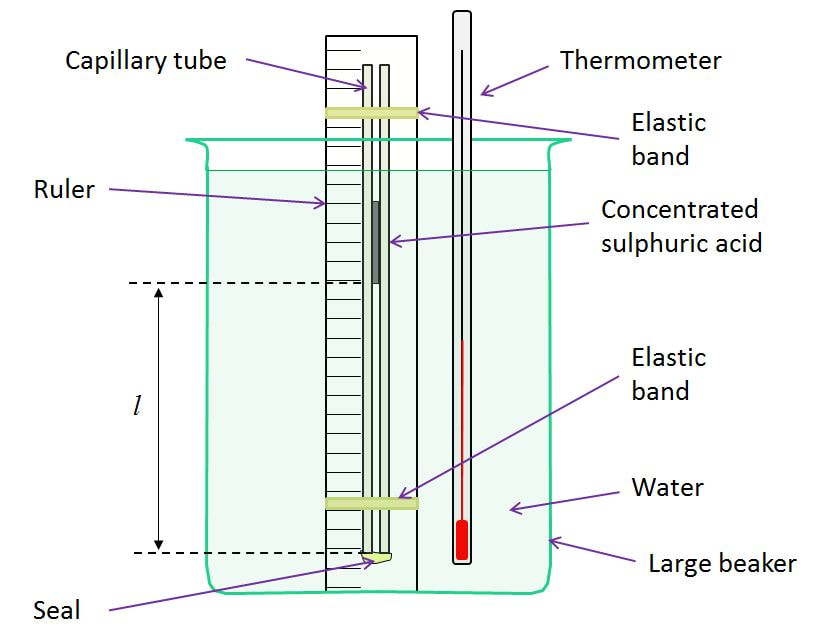
Charles' Law Lab We have a set of capillary tubes that are sealed at one end, and contain a small amount of oil inside, so as to trap a long bubble of air. These are taped to stainless steel rulers. As the bubble is heated it is free to expand at atmospheric pressure. Once placed in a water bath, the temperature and the length (i.e. volume) can be measured. Plotting the graph should yield similar results as for the pressure law. This tends not to be as accurate though, probably as the heating is usually too fast. |
LAB 12.2 - The Gas Laws
Universal Gas Law
It did not take the clever scientists very long to realise that all three of these laws could be easily and conveniently combined to form one ‘Universal Gas Law’. Setting any variable to be a constant, reduces the universal equation to one of the other gas law equations.
\[\frac{P_{1}V_{1}}{T_{1}}= \frac{P_{2}V_{2}}{T_{2}}\]
It did not take the clever scientists very long to realise that all three of these laws could be easily and conveniently combined to form one ‘Universal Gas Law’. Setting any variable to be a constant, reduces the universal equation to one of the other gas law equations.
\[\frac{P_{1}V_{1}}{T_{1}}= \frac{P_{2}V_{2}}{T_{2}}\]
Caveat:
Strictly speaking these gas laws only work for so-called ideal gases – i.e. ones that do not condense or chemically combine as they are compressed. A common example of a non-ideal gas would be steam or water vapour, because as it is compressed or cooled, it will condense to water and the volume and/or pressure will rapidly drop. This is the trick behind the famous egg-in-flask or crushing-can demonstrations that you will have seen.
Strictly speaking these gas laws only work for so-called ideal gases – i.e. ones that do not condense or chemically combine as they are compressed. A common example of a non-ideal gas would be steam or water vapour, because as it is compressed or cooled, it will condense to water and the volume and/or pressure will rapidly drop. This is the trick behind the famous egg-in-flask or crushing-can demonstrations that you will have seen.
2.5 - The Ideal Gas Law
Objectives:
- To know that the universal gas law is a simplification of the ideal gas equation \(PV = nRT\).
- To know that the internal energy of a gas is the sum of the \(KE\) of all the moving particles.
- Understand the qualitative relationship between the temperature and internal energy of a fixed mass of gas.
- To know that the internal energy can be determined by \(U = N \times KE = \frac{3}{2} nRT\)
The gas laws above are comparison equations, where is a variable changes we can determine how it affects other variables. We use these a lot in physics - e.g. moments, momentum etc. If the equation was to be made absolute we would get the following:
\[\frac{PV}{T}=constant\]
The value of this constant is based on TWO factors, a) the amount of the gas and b) the units of measurement that we are employing. The best way to express the amount of the gas in the container is by using the number of moles \(n\) and by keeping with the standard metric units for \(P\), \(V\) and \(T\) we get the so-called Gas Constant \(R = 8.31 \,\text{J/K mole}\).
\[PV = nRT\]
\[\frac{PV}{T}=constant\]
The value of this constant is based on TWO factors, a) the amount of the gas and b) the units of measurement that we are employing. The best way to express the amount of the gas in the container is by using the number of moles \(n\) and by keeping with the standard metric units for \(P\), \(V\) and \(T\) we get the so-called Gas Constant \(R = 8.31 \,\text{J/K mole}\).
\[PV = nRT\]
The above equation is the macroscopic equation for a gas - surprisingly, it is for every gas. It does not matter whether the gas is hydrogen, oxygen or propane. This result, known as Avogadro's Law, is due to the fact that the spacing between the particles that make up the up are far greater than the size of the particles themselves. However, the mass of the gas will vary. If we zoom in to consider the particles whizzing around inside the gas, we are looking at the Kinetic Theory. The name comes from the kinetic energy of the particles as they whizz about. The temperature of the gas is proportional to the average KE of the particles. A useful quantity is the INTERNAL ENERGY of the gas, which is essentially the sum of all the KEs of the individual particles. Since these are impossible to count and measure, we simply multiply the number of particles by the mean KE. The number of particles is defined as number of moles x Avogadro's number. The derivation of the equation can be found in a textbook, but essentially it is based on the work-energy principle and the conservation of momentum of colliding particles. The "3/2" coefficient is due to there being three dimensions, and the fact that the change in momentum from an elastic collision with a wall is twice the incoming momentum. What is key is the result that the internal energy of a gas is directly proportional to its temperature.
\[U = \sum KE=\frac{3}{2}nRT\]
\[U = \sum KE=\frac{3}{2}nRT\]
So, we could go on to use this equation to calculate the actual speed of particles in a gas. Calculating the mean speed of hydrogen at atmospheric pressure and room temperature yields a result of \(19,000 \,\text{m/s}\). This exceeds the escape velocity of the Earth and explains why hydrogen gas is not found in the atmosphere. Oxygen is heavier and so moves slower to have the same mean KE, around \(500 \,\text{m/s}\). Still, it is kind of interesting to know that we are being bombarded by tiny oxygen and nitrogen molecules whizzing around at roughly \(1800 \,\text{km/hr}\).... ouch!
|
Making Bread and the Ideal Gas Law
When you mix flour, salt, yeast and water together and kneed it into a dough, the yeast starts anaerobic respiration and reproducing. This produces carbon dioxide molecules. These molecules cannot escape the dough due to the gluten strands starting to harden throughout the dough. The carbon dioxide molecules tend to gather in areas around where they were produced and form bubbles. As the number of molecules increases, the bubbles expand in size and the dough rises. Later, it is put into the oven to raise the temperature. As the number of \(CO_2\) molecules is essentially fixed, because the higher temperatures kill off the yeast, the increase in temperature causes an increase in both pressure and volume of the \(CO_2\) bubbles. The bread rises and the baking solidifies the gluten and starch around the bubbles. |
2.6 - The First Law of Thermodynamics
Objectives:
- Understand the concept of internal energy, \(U\).
- Understand the basic idea of a gas trapped in a piston.
- Understand the two ways that we can increase the internal energy/temperature of a fixed mass of gas.
- Be able to use a \(p-V\) diagram.
- To understand and be able to use the First Law of Thermodynamics.
- To be able to relate the changes in a fixed mass of gas to the Gas Laws.
Thermodynamics is the science of the movement of heat energy into and out of a system (e.g. a fixed mass of gas). It is the key concept that is generally assessed at AP level. Historically, students can get bogged down in the signs of the variables and get confused by the diagrams/graphs.
The First Law of Thermodynamics is essentially the Law of Conservation of Energy. Energy cannot be created or destroyed, but merely transferred from place to place. Paraphrased it is: You can't get something for nothing.
In the context of thermodynamics, we will consider three forms of energy:
Sign convention - any process that raises the internal energy (i.e. temperature) of the gas is positive. The way to remember this is that a net energy flow into the gas raises the KE of the particles and hence the temperature.
The First Law of Thermodynamics is essentially the Law of Conservation of Energy. Energy cannot be created or destroyed, but merely transferred from place to place. Paraphrased it is: You can't get something for nothing.
In the context of thermodynamics, we will consider three forms of energy:
- Internal energy \(U\) of a gas, which is the overall KE of all the particles of the gas and is directly proportional to the temperature.
- Heat \(Q\), which is external energy that is either added to (heating) or removed (cooling) the gas.
- Work \(W\), which is performed when the gas expands or contracts. Imagine the piston being connected to a control rod and pushing or pulling something.
Sign convention - any process that raises the internal energy (i.e. temperature) of the gas is positive. The way to remember this is that a net energy flow into the gas raises the KE of the particles and hence the temperature.
|
The internal energy of a system can be increased by:
|
The internal energy of a system can be decreased by:
|
\[\Delta U = Q+W\]
The first law of thermodynamics is a classic example of basic physics. It is a law of simplicity that is easy to learn but sometimes very difficult to use. The first law of thermodynamics simply states that energy is conserved. Heat and work are just different ways of transferring energy. If we add up how much heat and work is transferred to a gas we will have found how much extra internal energy it now has.
When solving problems involving the first law of thermodynamics make sure that you know what is the system and what are its surroundings. Make sure that you know in which direction heat is being supplied and whether or not work is being done on the system or by the system.
The first law of thermodynamics is a classic example of basic physics. It is a law of simplicity that is easy to learn but sometimes very difficult to use. The first law of thermodynamics simply states that energy is conserved. Heat and work are just different ways of transferring energy. If we add up how much heat and work is transferred to a gas we will have found how much extra internal energy it now has.
When solving problems involving the first law of thermodynamics make sure that you know what is the system and what are its surroundings. Make sure that you know in which direction heat is being supplied and whether or not work is being done on the system or by the system.
CW12.5 - First Law
2.7 - Heat Engines and the Second Law
Objectives:
- Understand the concept of the second law of thermodynamics.
- Be able to describe the basic principle of a heat engine.
- Understand how the second law limits the efficiency of a heat engine.
- Be able to calculate the maximum efficiency of a heat engine.
So far we have used the first law of thermodynamics to learn about the changes to a system when heat is supplied or work is done. The first law tells us that we cannot get out more energy than we put in. We will now focus on the exchange of energy from heat-to-work and work-to-heat. When we rub our hands together it is easy to see that all of the work that we are doing is converted into heat, this process is easy. However, it is much harder to turn heat into useful work.
A heat engine is a cyclic device that takes in energy as heat and converts some of this energy to a more useful type (work). During this process the heat engine will also lose some energy by transferring heat to the surroundings.
A car is an example of a heat engine. Fuel is burnt and the energy released is converted into mechanical energy to move the car and generate electricity for ancillary devices. Some of the heat released in burning the fuel is lost through the exhaust. Because gases leave in the exhaust it is not a fully cyclic engine.
A heat engine is a cyclic device that takes in energy as heat and converts some of this energy to a more useful type (work). During this process the heat engine will also lose some energy by transferring heat to the surroundings.
A car is an example of a heat engine. Fuel is burnt and the energy released is converted into mechanical energy to move the car and generate electricity for ancillary devices. Some of the heat released in burning the fuel is lost through the exhaust. Because gases leave in the exhaust it is not a fully cyclic engine.
|
|
|
|
|
Breaking the Second Law?!
|
Links