Hamilton on a calm night. The importance of electricity to our everyday lives is obvious. A hundred years ago this would have been in darkness.
|
This unit covers the interaction of charged particles, such as electrons, and low voltage direct
current circuits, which are common in cars, boats and battery operated equipment.
Students are expected to be able to calculate the voltages across components, the current flowing through the circuits and the energy transferred per second. Series and parallel circuits are considered, as combinations of both. The difference between the terminal voltage of a cell and its emf is explained by considering the internal resistance of a cell, which is an important way of determining the "health" of a battery. |
|
10.1 - Basic Concepts
|
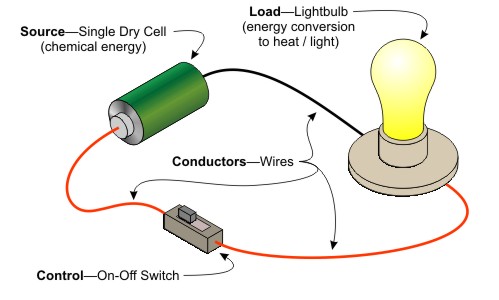
Electricity is the flow of electrons around a circuit. Electrons are only 'free' to move in conducting materials such as metals, ionic solutions and graphite - although at AP-1 we confine ourselves purely to metals as they are the materials used in building circuits. The electrons 'hop-skip-jump' from one atom to the next, but can only move if there is a space to go to and if another electron will replace it. This can be imagined as a circle of students passing tennis balls around and around. Any break whatosever and the current stops. The actual speed of the electrons is very slow - only mm/s, but as all the electrons effectively move simulateously, the current appears instant.
Electrons are very, very small and carry a tiny electrical charge. An American scientist determined the charge on the electron to be quantised - i.e. that it was the same. Every electron has an identical electrical charge. This is called "e". (Not to be confused with Euler's number.) As all electrostatic charges are caused by a whole number of electrons, all electrical charges must be an integer multiple of e. In practice, the charge flowing in a circuit is so high that this is not an issue. Occasionally you may encounter a multiple choice question that states a charge on particle and asks whether it is possible or not...
\[e= -1.6\times 10^{-19}\: \text{C}\]
The current itself is related to a) how fast the electrons are moving and b) how many electrons there are. It is the rate of flow of electrons. Generally the number of electrons flowing though a bulb per second is vast, too large a number to be useful. Therefore, we define a unit of charge called the Coulomb. There are an awful lot of electrons per Coulomb of charge!
\[1\: \text{C}= 6.24 \times 10^{18}\: \text{electrons}\]
The current, I, is defined as the rate of flow of charge , Q, around the circuit. The unit was named the Ampere, usually shortened to Amp (A) after Henri Ampere who did a lot of work on electricity and magnetism. It can be measured using a device called an ammeter. This will be familar to you already!
\[I=\frac{\Delta Q}{t}\]
The voltage (potential difference) provided by a cell or battery provides the 'push and pull' to induce the electrons to move. The positive side of the cell attracts the electrons and the negative side repels them. The higher the voltage, the faster the electrons move. The voltage gives the electrons energy and it is this energy that is transfered in an electrical circuit. Voltage is measure using a voltmeter. The units are Volts (V). The unit and varaible symbols are both "V". When typed, the variable is italicised. In practice this is not as confusing as may be expected. Named afterAlessandro Volta, who invented the battery. 1 volt = 1 joule of energy per coulomb of charge. It is straightforward to calculate how much energy is given by a 1.5 V battery to each teeny electron - not very much.
\[V=\frac{E}{Q}\]
Electrons are very, very small and carry a tiny electrical charge. An American scientist determined the charge on the electron to be quantised - i.e. that it was the same. Every electron has an identical electrical charge. This is called "e". (Not to be confused with Euler's number.) As all electrostatic charges are caused by a whole number of electrons, all electrical charges must be an integer multiple of e. In practice, the charge flowing in a circuit is so high that this is not an issue. Occasionally you may encounter a multiple choice question that states a charge on particle and asks whether it is possible or not...
\[e= -1.6\times 10^{-19}\: \text{C}\]
The current itself is related to a) how fast the electrons are moving and b) how many electrons there are. It is the rate of flow of electrons. Generally the number of electrons flowing though a bulb per second is vast, too large a number to be useful. Therefore, we define a unit of charge called the Coulomb. There are an awful lot of electrons per Coulomb of charge!
\[1\: \text{C}= 6.24 \times 10^{18}\: \text{electrons}\]
The current, I, is defined as the rate of flow of charge , Q, around the circuit. The unit was named the Ampere, usually shortened to Amp (A) after Henri Ampere who did a lot of work on electricity and magnetism. It can be measured using a device called an ammeter. This will be familar to you already!
\[I=\frac{\Delta Q}{t}\]
The voltage (potential difference) provided by a cell or battery provides the 'push and pull' to induce the electrons to move. The positive side of the cell attracts the electrons and the negative side repels them. The higher the voltage, the faster the electrons move. The voltage gives the electrons energy and it is this energy that is transfered in an electrical circuit. Voltage is measure using a voltmeter. The units are Volts (V). The unit and varaible symbols are both "V". When typed, the variable is italicised. In practice this is not as confusing as may be expected. Named afterAlessandro Volta, who invented the battery. 1 volt = 1 joule of energy per coulomb of charge. It is straightforward to calculate how much energy is given by a 1.5 V battery to each teeny electron - not very much.
\[V=\frac{E}{Q}\]
|
|
|
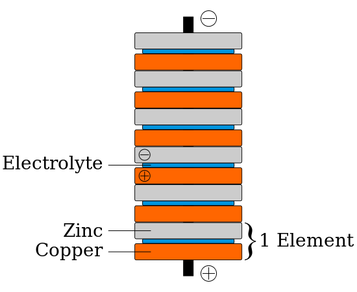
The battery (voltaic pile) invented and built by Volta. It is easy to make this at home using copper coins, aluminium foil and paper soaked in vinegar. Volta realised that a battery can be made from any dissimilar metals (electrode) separated by a conducting solution (electrolyte).
10.2 - Resistance and Ohm's Law
|
If the cell was to keep pushing and pulling the electrons around the circuit and there was nothing impeding their movement, their speed would quickly escalate. There is something that hinders them though and this is known as resistance. I tend to think of resistance as the "friction" inside a circuit. Like friction, resistance converts the motion of the electrons to heat. Like friction, the higher the resistance, the slower the electrons move. It is not caused by friction though - but that is another story for another day. The current that flows is proportional to the voltage applied and inversely proportional to what is opposing it.
\[I = \frac{V}{R}\]
Which is usually remembered in its rearranged form:
\[V=IR\]
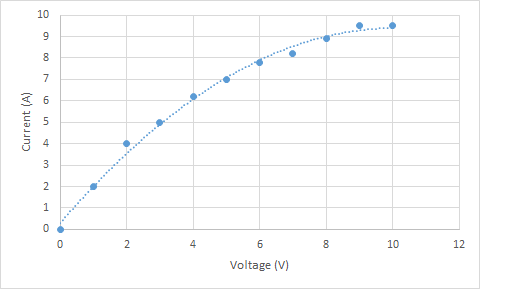
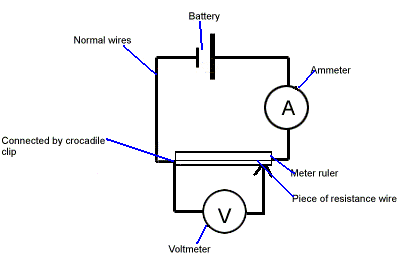
This is known as Ohm's Law and is fundamental. Experimentally, resistance can be determined by varying the voltage, recording the current and plotting a graph. This yields a straight line graph if the resistance is constant. For some components the resistance varies. The most common being an old-fashioned light bulb. The filament of which gets VERY hot. As its temperature increases, the resistance increases too.
\[I = \frac{V}{R}\]
Which is usually remembered in its rearranged form:
\[V=IR\]
This is known as Ohm's Law and is fundamental. Experimentally, resistance can be determined by varying the voltage, recording the current and plotting a graph. This yields a straight line graph if the resistance is constant. For some components the resistance varies. The most common being an old-fashioned light bulb. The filament of which gets VERY hot. As its temperature increases, the resistance increases too.
|
|
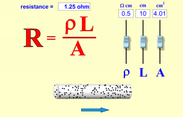
The resistance of a wire depends on three variables:
- the length of the wire, the longer it is the higher the resistance
- the thickness of the wire, the higher the cross-sectional area the lower the resistance
- the material of the wire, the resistivity. Copper has a lower resistivity than ni-chrome alloy.
|
You will have done this experiment at IGCSE but we will do a shortened version of it again at AP-1 to determine a value for a material's resistivity and compare with the textbook values. We will also be re-doing the light bulb experiment.
\[R=\frac{\rho L}{A}\] LAB 10.x1
LAB 10.x2 LAB 10.x3 |
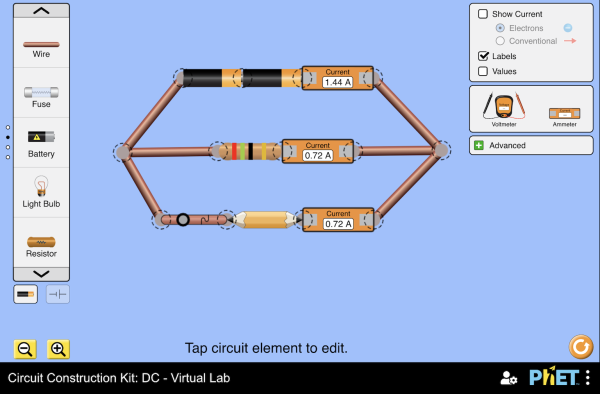
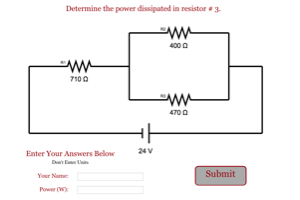
10.3 - Resistors in Series and Parallel
|
| Click to Run |
10.4 - Internal Resistance and emf
|
|
Physics Aviary Problem
|
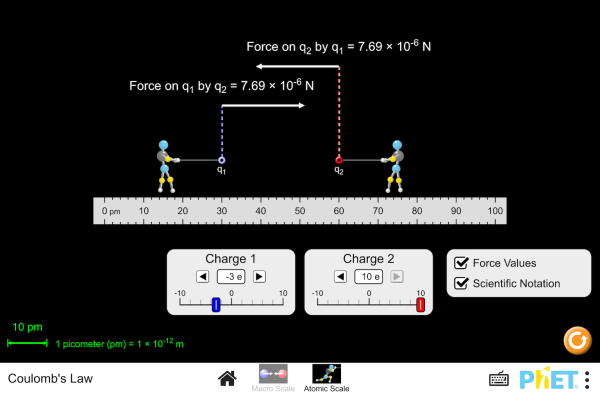
10.5 - Coulomb's Law
|
| Click to Run |
